プロスペクト理論シリーズ目次
- プロスペクト理論を数式と原典からガチ解説
- 確率重み関数で読み解くプロスペクト理論
- 損失回避の損は得の2倍の出どころ ← 今ここ
導入:あなたは「フェアな賭け」を受けますか?
コイン投げで勝てば1万円もらえる。負けたら1万円払う。確率は五分五分。期待値ゼロの「フェアな賭け」──合理的に考えれば、乗っても乗らなくても同じはで。でも、多くの人はこの賭けを「嫌だ」と感じます。
「損失回避」の話だ、と聞いたことがある人は多いでしょう。「損は得の2倍に感じる」「2.25」という数字も、どこかで見たことがあるかもしれません。では、その「2倍」や「2.25」は、いったいどこから来た数字なのでしょうか?
本記事では、プロスペクト理論の原典──Kahneman & Tversky(1979)とTversky & Kahneman(1992)──を追いながら、その出どころを特定していきます。
1979年論文(Kahneman & Tversky)
- 人は「最終資産」ではなく「変化(得/損)」で評価する(Coding)
- その基準が「参照点」──多くは現状だが、期待や願望が参照点になることも
- 損失側の価値関数は利得側より急 = “losses loom larger than gains”
- 定性的主張のみ。「2倍」という数字はまだ出ない
1992年論文(Tversky & Kahneman)
- 混合くじ実験で「利得は損失の少なくとも2倍必要」と観察
- 価値関数パラメータを被験者ごとに非線形回帰で推定
- 中央値 λ=2.25(25名中13番目の人の値)
- 人類共通の定数ではなく、この実験の「真ん中の人」の値
第1章 1979年:損失回避の”骨格”は参照点とキンク(折れ曲がり)
Coding(符号化)という考え方
1979年論文の核心は、人がお金を評価するとき「最終的にいくら持っているか」ではなく、「今からいくら増えるか/減るか」で判断する、という主張です。論文ではこれを”Coding”と呼び、次のように述べています。
“people normally perceive outcomes as gains and losses, rather than as final states of wealth or welfare”(K&T 1979, p.274)
(人は結果を、富や福利の最終状態としてではなく、利得や損失として認識するのが普通である)
ここでいう「得か損か」を分ける基準が参照点(reference point)です。多くの場合は「現状」が参照点になりますが、期待や予測が参照点になることもあります。

「今100万円持ってて、110万円になるか90万円になるか」っていう見方じゃなくて、「プラス10万かマイナス10万か」で考えるってこと?

そうそう。人間は「絶対額」やなくて「変化量」に反応する。これがプロスペクト理論の出発点であり、大事な一撃や。本編の記事でもやったやろ?
参照点は「現状」だけじゃない
論文では、参照点が「現状」ではなく期待や願望になるケースも議論されています。これが面白いところで、同じ金額の変化でも「得」に見えたり「損」に見えたりする原因になります。
【① 期待との乖離】
毎月の給与から予期せぬ増税分が差し引かれた場合、それは「利得の減少」ではなく「損失」としてコーディングされる。
→ 手取り25万円を期待していたのに23万円だった → 「−2万円の損失」と感じる
【② 相対的な評価】
不況下にある起業家が、競合他社よりも被害を抑えられた場合、期待していた大きな損失と比較して、小さな損失を「利得」として解釈することがある。
→ 「100万円赤字」を覚悟していたのに「30万円赤字」で済んだ → 「+70万円の利得」と感じる
【③ 適応の遅れ】
過去に大きな損失を出したばかりで、まだその状況に心理的に適応できていない人は、現在の低い資産状況を参照点とせず、過去の資産状況を参照点として維持することがある。
→ 100万円損した直後に「50万円取り返せる五分五分の賭け」を持ちかけられると、「100万円のマイナスを50万円に減らすチャンス」としてコード化し、ギャンブル的な選択をしやすくなる

③の「適応の遅れ」って、競馬で負けた人が最終レースで大穴に全ツッパするやつやん…。一旦冷静になればええところ、参照点が追いついてないんやな。

まさにそれや。損失を取り返そうとして、よりリスキーな選択に走る。論文でも「損失に適応していない人は、そうでなければ受け入れられないような賭けを受け入れる可能性が高い」と書いてある。これが「損失域でのリスク愛好」の実態の一つや。
※参照点と価値関数の詳細はプロスペクト理論の本丸記事で書いています
→ 人間の不合理はこう曲がる|プロスペクト理論を数式と原典からガチ解説
“Losses loom larger than gains”の登場
1979年論文で、損失回避の核心が述べられます。
“losses loom larger than gains”(K&T 1979, p.279)
(損失は利得よりも大きく迫ってくる)
つまり、同じ金額でも、もらうより失う方が心理的インパクトが大きいということです。この論文では、対称的な賭け(勝てば+x、負ければ−xの五分五分)が嫌われることを根拠に、価値関数の損失側の傾きが利得側より急であることを示しました。
論文のFigure 3には、有名なS字型の価値関数が描かれています。原点(参照点)を境に、右上が利得、左下が損失。損失側のカーブが利得側より急なのがポイントです。自作した価値観数を提示しておきます。
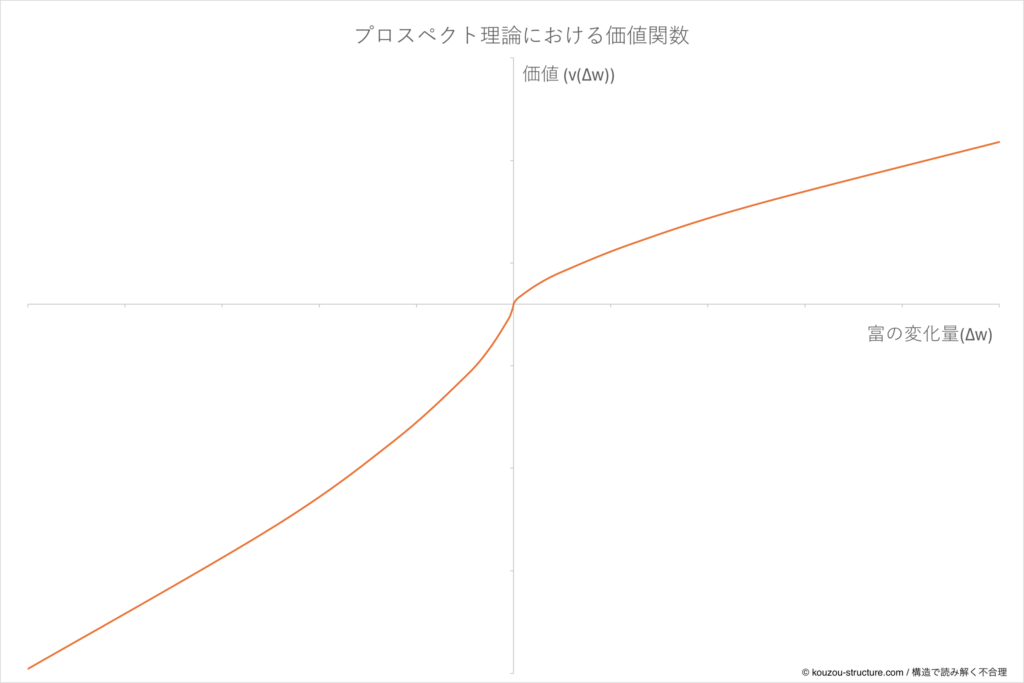

1979年のときには「2倍」とは言ってないんやね。

言ってへん。「急」とか「steeper」とか、定性的な話だけやな。数字が出てくるのは1992年を待たなあかん。それでも本質は捉えとるな。
第2章 1992年:「2倍」の直接の出どころ
混合くじを「受け入れ可能」に調整させる課題
1979年論文では「損失は利得より重い」という定性的な主張が示されましたが、「どれくらい重いのか」は明らかにされていませんでした。1992年論文では、その「重さ」を数値で捉えるための実験が行われています。
実験の狙いはシンプルです。「損の痛み」を直接測りに行く。
具体的には、被験者に「損失が固定された混合くじ」を提示し、「いくらの利得がセットになっていれば、この賭けを受けてもいいと思えるか」を答えさせました。もし損失と利得が同じ重さで感じられるなら、答えは損失額と同額になるはず。でも実際は——損失額の約2倍の利得を要求した。これが「損は得の2倍」の直接的な観察データです。
鍵になるのはTable 6の実験です。この実験の設計を丁寧に見ていきましょう。
【実験の問い】
「50%の確率で$x もらえて、50%の確率で$25 失う。
いくら以上もらえるなら、この賭けを受けてもいいと思う?」
つまり、損失額は固定($25、$50、$100、$150)しておき、「それでも賭けていいと思える最低限の利得額」を被験者自身に決めさせたのです。

「25ドル負けるかもしれんけど、いくらもらえるなら乗ってもええ?」ってことか。

せや。期待値だけで考えるなら、25ドル失うリスクには25ドル以上の利得があればトントンやけど…人間はそうは答えへんかったんや。
【なぜこれで損失回避がわかるのか】
もし人間が「得も損も同じ重さ」で評価するなら、答えは損失額と同じになるはずです。
でも実際は、損失額よりはるかに大きな利得を要求した。これが「損失は利得より重く感じる」=損失回避の直接的な証拠です。
【実際の結果(Table 6 Problem 1-4)】
| Problem | 損失(固定) | 利得(中央値) | 比率 |
|---|---|---|---|
| 1 | $25 | $61 | 2.44 |
| 2 | $50 | $101 | 2.02 |
| 3 | $100 | $202 | 2.02 |
| 4 | $150 | $280 | 1.87 |
Table6の厳密な実験設計(クリックで展開)
本来は被験者に「AとB、2つのくじが同じくらい魅力的に見えるx」を答えさせています。
・くじA:確実に$0(何もしない)
・くじB:50%で $−c を失い、50%で $x を得る
problem4まではクジAが0$だけなので、あえて簡略化した書き方をしています。原典ではくじAを更に調整した結果も表記されていますが、今回は損失回避が主眼であるため、意図的に省略します。
論文ではこの結果を次のようにまとめています。
“for even chances to win and lose, a prospect will only be acceptable if the gain is at least twice as large as the loss”(T&K 1992, p.310)
(勝ち負けが五分五分の賭けでは、利得が損失の少なくとも2倍以上でないと、その賭けは受け入れられない)
これが「損は得の2倍」の直接の出どころです。課題の中央値から導かれた「観察結果」であり、理論から演繹された定数ではありません。

25ドル失うかもしれんのに、61ドルもらえんと嫌やというこっちゃな。約2.4倍やん。

せやねん。損失$50に対しては$101、$100に対しては$202、$150に対しては$280…と、だいたい「損失の2倍前後」の利得がないと受け入れられへんかった。
第3章 1992年:「λ=2.25」の出どころ(ここが本丸)
価値関数のパラメータ推定
1992年論文では、価値関数を次の形で定式化しています。詳細はプロスペクト理論本編をどうぞ。
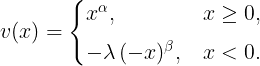
利得側: v(x) = x^α (x ≥ 0のとき)
損失側: v(x) = −λ(−x)^β (x < 0のとき)
ここでλ(ラムダ)が「損失回避係数」です。λが大きいほど、損失側の傾きが急になり、損失回避が強いことを意味します。

本編の記事で出てきたα・β・λやな。αとβが「頭打ちの曲がり具合」で、λが「損の重み」やったっけ。

せや。で、このλをどうやって見つけたかが今回のポイントや。
推定結果:中央値λ=2.25
推定の手順:「一人ひとりにフィットして、その中央値を取る」
ここが重要なポイントです。λ=2.25は「全員のデータをまとめて一緒に分析した」のではありません。実際の手順は以下の通りです。
- 25名の被験者それぞれに、多数のくじ選択課題をやらせる
- 一人ごとに、上述の価値関数の式に当てはめて、その人のα・β・λを推定(非線形回帰)
- 25人分のλが出そろったら、その中央値を取る

「非線形回帰」ってなんや?難しい言葉やめてくれ。

簡単に言うと「その人の選択パターンに一番合うように、さっき出した式のα・β・λの値を調整する」ってことや。価値関数の形が曲線やから「非線形」やね。

つまり「この人はλ=1.8」「この人はλ=2.5」みたいに、一人ひとり違うλとかαが出てくるわけやな。

そういうこと。そしてその25人分のλを小さい順に並べて、13番目(真ん中)の人の値が「中央値」や。平均値やないで。これが「λ=2.25」の正体や。
この手順を論文では次のように述べています:
つまり、λ=2.25は「人類の損失回避係数」ではなく、この実験の25人の「真ん中の人」の値にすぎません。以下が本編でも提示した、1992論文からの定数中央値です。
| パラメータ | 中央値 | 意味 |
|---|---|---|
| α | 0.88 | 利得側の曲率(頭打ち) |
| β | 0.88 | 損失側の曲率(ヤケクソカーブ) |
| λ | 2.25 | 損失回避係数 |

「中央値」ってことは、25人のうち真ん中の人の値ってこと?なんで平均値やないんやろな。

そういうこと。25人を大きい順に並べて13番目の人の数字やな。平均値やないし、ましてや「人類共通の定数」なんかやないな。損失にビビりまくる人もいれば、ケロっとしているひともいるやろ。そういう極端な人を含めて平均値使うと、値がその人に引っ張られる可能性があるから、中央値にしたんやないかな。
1992年までの限界:「いつでも2倍」ではない
ここまで見てきたように、1979年論文で「損失は利得より重い」という定性的主張が登場し、1992年論文でそれが「約2倍」「λ=2.25」という数字で定量化されました。
素朴な疑問:支払いは「損失」じゃないのか?
ここで素朴な疑問が浮かびます。「お金を失う=損失」なら、買い物をするたびに損失回避が発動するはずです。コンビニで100円支払うたびに「うわぁ2倍、200円分の痛みだ!」と感じるはずです。
でも、実際はどうでしょうか。毎日コーヒーを買っても、サブスクの引き落としがあっても、そこまで「損した」とは感じません。支払いは確かにお金が出ていくけれど、それほど痛みを感じない。これはなぜでしょうか?
もし損失回避が「いつでも・どこでも・どんな状況でも」発動するなら、日常の買い物は地獄のはずです。100円のおにぎりを買うたびに200円分の心理的ダメージを受け、月額1,000円のサブスクで毎月2,000円分の痛みを感じる——そんな人は、まともに経済生活を送れません。でも、私たちは毎日買い物をしています。それなりに平気で。
1979年・1992年が答えていないこと
1979年論文と1992年論文は、損失回避の存在と大きさを示しました。しかし、「どんな条件で発動し、どんな条件で発動しにくいのか」という境界条件(boundary conditions)については、ほとんど触れていません。
この宿題に取り組んだのが後続研究があります。次回この話に取り掛かります。
まとめ:由来の最短ルート
1979年(Kahneman & Tversky)
- 人は結果を「最終資産」ではなく「変化(得/損)」として評価する
- その基準が「参照点(reference point)」
- 損失側の傾きは利得側より急= “losses loom larger than gains”
- 数字はまだ出ない
1992年(Tversky & Kahneman)
- 混合くじの調整課題で「利得は損失の少なくとも2倍必要」と観察
- 価値関数のパラメータ推定で「中央値 λ=2.25」を算出
- ただし25名の中央値であり、人類定数ではない
「損は得の2倍」──このフレーズが独り歩きしていますが、その出どころは1992年論文の特定の実験課題と推定結果でした。人類普遍の定数ではなく、「だいたいこれくらい」という経験的な目安として理解しておくのが正確です。
執筆後記
1992年論文を読んでいて、ひとつ気になったことがあります。λ=2.25という数字は「25名の中央値」と報告されていますが、その散らばり具合(標準偏差、最小値・最大値など)は一切示されていません。本音を言うと、記事を書くに当たってはばらつきの正確なデータは欲しかったです。
中央値で報告しているということは、おそらく分布が歪んでいたか、外れ値の影響を避けたかったのだろうと推測はしています。しかし、実際にどれくらい個人差があったのか──λが1.5から3.5まで幅広く散らばっていたのか、それとも2.0〜2.5あたりに集中していたのか──は、この論文だけでは判断できません。
まあそもそも、この実験の被験者はバークレーとスタンフォードの大学院生25名だけです。サンプルサイズも属性も限定的で、「人類一般の損失回避」を語るには心許ない土台ではあります。問いの形や状況で変わるでしょう。この辺りは後続研究のターゲットにもなっていますね。
一方で、同じ論文のTable 4(p.308)には、確率加重関数に関する25名分の個人別データが載っていて、そちらはかなりの個人差が見て取れます。損失回避のλについても同様のばらつきがあったのではないか、というのが私見です。
λ=2.25という数字は便利な目安ですが、「ある実験の真ん中の人の値」であり、その周囲にどれだけの幅があったかは、少なくともこの論文からは読み取れない──そのことは心に留めておいてよいと思います。
参考文献
- Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47(2), 263–291.
- Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5(4), 297–323.




コメント