- 導入｜「ホモ・エコノミクス」とノーベル賞のあいだにあるモヤモヤ
- 第1章 ホモ・エコノミクス業界の2派閥｜「期待効用理論」のどこまでが限界か
- 第2章 純血派ホモエコと期待効用理論｜直線効用だけで世界を説明しようとすると
- 第3章 修正派ホモエコ｜限界効用逓減だけでは説明できないこと
- 第4章 プロスペクト理論の価値関数 v(Δw)｜損失回避とS字カーブ
- 第5章 プロスペクト理論の確率重み関数 π(p)｜低確率を盛りすぎる人間
- 第6章 プロスペクト理論のパラメータ αβγλ｜人間のクセを蒸留した4つのノブ
- 第7章 実験経済学とプロスペクト理論｜カーネマンとバーノン・スミスの接点
- 第8章 まとめ｜ホモ・エコノミクスとプロスペクト理論の違いを一枚に整理
- 参考文献
- 関連記事
導入｜「ホモ・エコノミクス」とノーベル賞のあいだにあるモヤモヤ
行動経済学の本を読んでいると、「プロスペクト理論」「カーネマンはノーベル賞を取った」というフレーズがイヤというほど出てきます。でも、ふと立ち止まって考えると、こんな疑問が残りませんか？
- なぜ、この理論がそれほど評価されたのか？
- 既存の期待効用理論（ホモ・エコノミクス）と、具体的にどこが違うのか？
多くの本や解説記事は、一枚のグラフだけ見せて終わります。そう、有名なＳ字曲線です。左右が頭打ちになり、損失側の傾きがきつくなっているあのグラフ。なぜそのグラフが描き出されたのかを解説した記事を、私は見たことがありません。
この記事では、ガチガチのホモ・エコノミクスの直線からスタートし、そこに少しずつ「人間味」を足していき、最終的にプロスペクト理論のS字＋確率の歪みまで持っていきます。さらに、
- カーネマン＆トヴェルスキーはどのようにグラフのパラメータを見出したのか
- そのアプローチが、ノーベル経済学賞同時受賞のバーノン・スミスの実験経済学と構造的に同じであること
まで含めて、「だからこの理論とこの二人でノーベル賞」というところまで一本の線でつなぎます。
ベースにするのは以下
- 1979年の Prospect Theory（オリジナルPT）
- 1992年の Advances in Prospect Theory（累積プロスペクト理論／CPT）
- 2002年ノーベル経済学賞受賞時のプレスリリース
身構える必要はありません。数式は出しますが、高校レベルで追える範囲にとどめます。「直線がS字に曲がるまで」をできるだけわかりやすく解説します。数式がわからなくても、直感で理解できるよう表現を工夫しました。ぜひお付き合いください。
専門家の方へ（ご挨拶とお願い）
本記事では、プロスペクト理論の「直感の骨格」を一般向けに伝えることを優先し意図的な単純化・雑な書き方 をしています。学部〜大学院レベルで勉強されている方から見ると、「そこはもう少しちゃんと書けるやろ」というところが多々あると思いますが、「非専門家がプロスペクト理論の根幹を見に行く踏み台」という位置づけで割り切って構成しました。もし 明らかにミスっている箇所 や、「ここだけはさすがに誤解を生む」というポイントがありましたら、お手数ですがご指摘いただけると大変ありがたいです。可能な限り原典に沿う形で順次修正していきます。
第1章 ホモ・エコノミクス業界の2派閥｜「期待効用理論」のどこまでが限界か
まずは、ホモ・エコノミクス界隈の内部事情から。ここを押さえた方が、プロスペクト理論の「立ち位置」が一気にクリアになります。ホモ・エコノミクスであるエコノさんに解説させます
まずな、ワイら「ホモ・エコノミクス」の世界の中にも派閥があってな。ざっくり言うとホモエコ内部に2派閥。で、その外側に「実際の人間」を説明しに行く理論がおる、という感じや。以下にまとめるで。
- 純血派ホモエコ（原理主義）
- 修正派ホモエコ（頭打ちだけ入れたやつら）
- 実際の人間を数式でとらえようとした派（プロスペクト理論）
以上３つを押させておくと、次からの理解がしやすい。頭に置いておきましょう。
コラム：この先で出てくる「記号たち」の道具箱
ここから先、数式や記号がちょこちょこ出てきます。といっても高校数学＋ちょい記号レベルなので、ここだけ押さえておけば大丈夫です。わからなくなったら、いったんここに戻ってきてもらえればOK。
1. お金まわり
- w : wealth（富） いま持っているお金・財産の大きさだと思ってください。
- Δw : change in wealth（富の変化） 「いくら持ってるか」ではなく、どれだけ増えたか／減ったか。
2. 感じ方（効用・価値）
- u : utility（効用） 伝統的な経済学が使う「ホモエコの満足度メーター」。
- v : value（価値） プロスペクト理論側の「人間の満足度メーター」。
3. 確率まわり
- p : probability（確率） 客観的な確率そのもの。「サイコロで1が出る確率 p = 1/6」のようなもの。
- π(p) : weighted probability（確率の“効き目”） 人間が体感している方の確率。
第2章 純血派ホモエコと期待効用理論｜直線効用だけで世界を説明しようとすると
2-1. まずは「期待値マン」の頭の中をのぞく
純血派ホモエコの世界では、すべての判断が「期待値」という一つの物差しで決まります。ちょっとだけ丁寧にいきましょう。
期待値ってそもそも何？
具体例から。
- A案：1万円を100%の確率でもらえるくじ
- B案：2万円を50%、0円を50%の確率でもらえるくじ
普通に考えると、
- A案の「平均的にもらえる金額」= 1万円 × 100% = 1万円
- B案の「平均的にもらえる金額」= 2万円 × 50% + 0円 × 50%= 1万円
どちらも 平均すると 1万円 ですよね。この「起こりうる金額 × その確率 を全部足し合わせたもの」を、ホモエコたちは 期待値 と呼びます。
純血派ホモエコの評価ルール
この世界では、どんな選択肢でも「起こりうる金額 × その確率」を全部掛け算して足し合わせる→ その合計が大きい方が“正しい選択”
というルールだけで動きます。
- 結果：最終的な富（お金の量） w
- その結果が起こる確率：p
とすると、「ホモエコ的な評価」＝「その選択肢の期待値」ということになります。
2-2. 直線効用：お金1円＝うれしさ1ポイント
ここで、さっきの「満足度メーター」の話に戻ります。純血派ホモエコは、お金と満足度の関係を「完全な直線」として扱う人たちです。
- お金が1万円 → 満足度 1万ポイント
- お金が2万円 → 満足度 2万ポイント
みたいなノリで、「1円増えると、どこまでいっても“同じだけ”うれしくなる」と考えます。
数式っぽく書くと：
u(w) = w（u：効用、w：お金の量）
グラフにするとこんなイメージです。
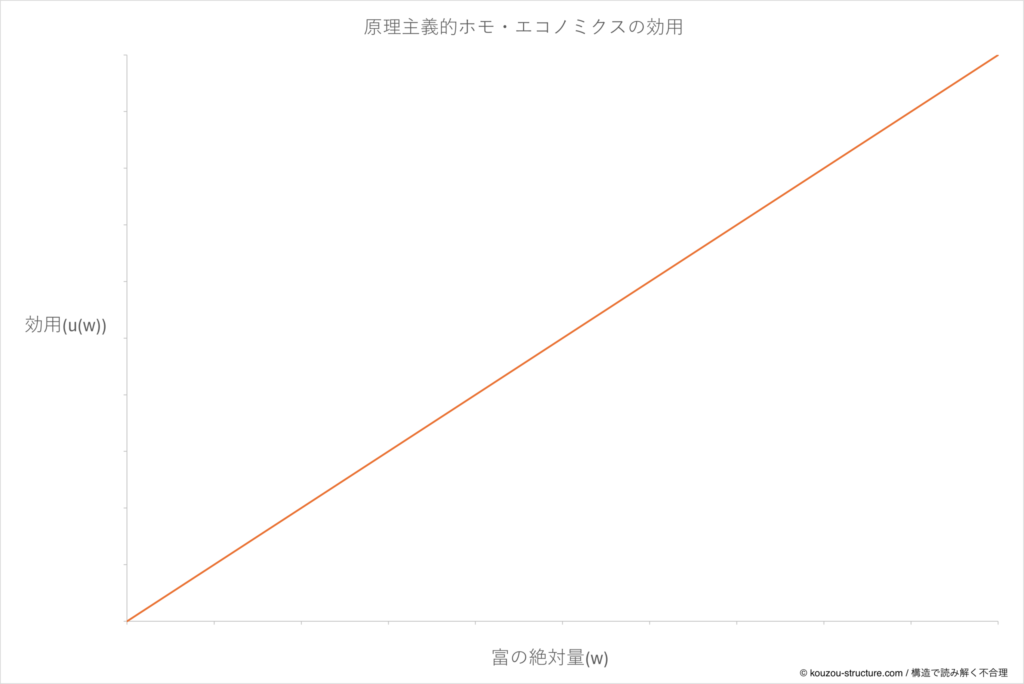
- 横軸：お金の量 w
- 縦軸：満足度 u(w)
右上に向かって、きれいな直線が一本スッと伸びているだけ。
つまり、「今の貯金が1億あろうが10万円だろうが、同じ1万円なら同じだけうれしい」ってこと？
そういうこっちゃ。人によって違うとか、状況によって違うとか、そういう人間くささは一回全部捨てとるねん。
2-3. 純血派ホモエコの世界線で起こること
この「期待値マン＋直線効用」の組み合わせで世界を見ると、だいたいこんな行動パターンになります。
- 宝くじ→ 期待値はほぼ確実にマイナス「買うやつは全員非合理、以上」
- 延長保証や各種保険→ 多くは「払うお金 ＞ 期待される補償」→ 「基本的に全部入るべきではない」
- ローンの繰り上げ返済 vs 投資→ 期待リターンが高い方だけを見る→ リスクや気持ちの安心感は、評価に入ってこない
- 現実の人間が「期待値が低い選択」をしたら、「人間の方が間違っている」とみなす。
いやいや、宝くじ買ったり保険入ったりする人、世の中に山ほどおるやん……
せやから純血派からしたら、「みんな非合理」「勉強が足りん」で話が終わるねん。
2-4. どこがイケてそうで、どこがヤバいか
純血派ホモエコの世界観には、「きれいさ」と「ヤバさ」が同居しています。
- きれいなところ
- ルールが超シンプル：「期待値が高い方を選べ」
- 数学的に扱いやすい（直線だし、平均取るだけだし）
- 理論としてはスッキリしていて、美しい
- ヤバいところ
- お金1円の価値が、「貧乏な人」でも「大富豪」でも「今日破産した直後」でもまったく同じ という前提になっている
- 宝くじ・保険・延長保証みたいなものを買う人は、全員「間違っている」扱いになる
第3章 修正派ホモエコ｜限界効用逓減だけでは説明できないこと
3-1. 効用にだけ人間味を足す
第2章の純血派ホモエコは、「お金が増えた分だけ、満足度もキレイに一直線で増える」という世界に住んでいました。さすがにそれはムリがあるやろ…と考えたのが、修正派ホモエコです。彼らの感覚はだいたいこうです。
「お金は増えれば増えるほど嬉しい。でも、1,000円→1万円と、1万円→10万円では“嬉しさの増え方”は全然ちゃうやろ？」この「だんだん頭打ちになる感じ」を数式に入れたのが、次の形です。
u(w) = w^α （0 < α < 1）
- α = 1 第2章の純血派と同じ“直線”
- α < 1 右肩上がりだけど、だんだん寝てくる“上に凹んだカーブ”
グラフで書くと
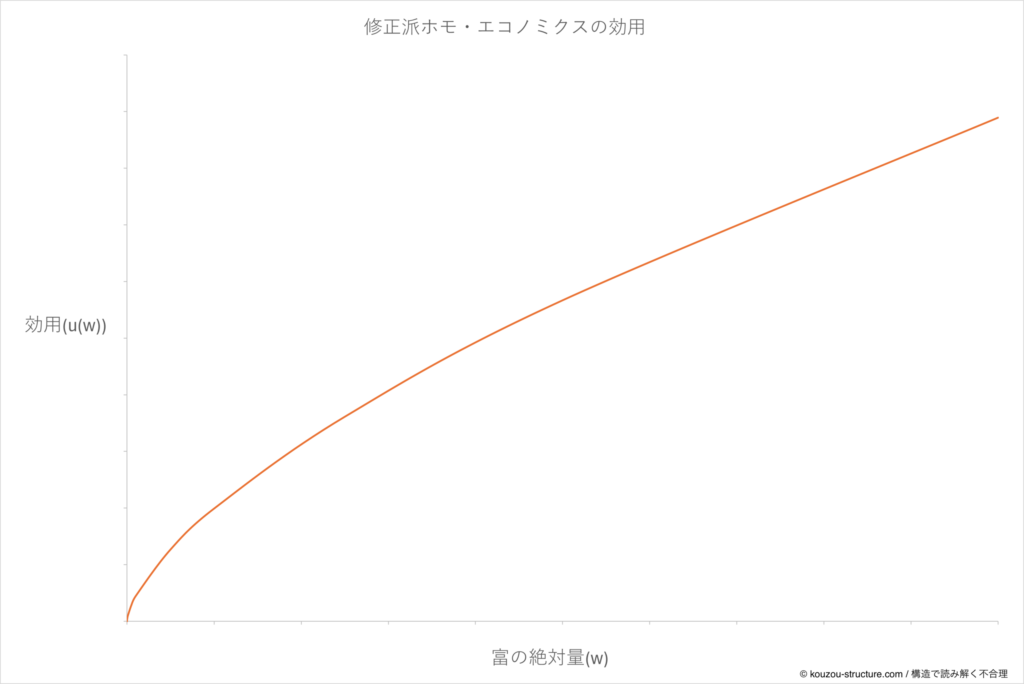
- 最初の1万円 → うれしさドーン！
- 2万円目 → うれしいけど、「最初ほどではない」
- 3万円目 → さらにうれしいけど、やっぱり「増え方は鈍る」
みたいな「限界効用逓減（げんかいこうようていげん）」を素直に反映した形です。
3-1-2. 評価ルールはそのまま「期待値マン」
ここで大事なのは、「お金 → 満足度」の変換だけを曲げたという点です。
- 見ているのは、相変わらず「最終的な富 w」
- 確率も、そのまま p を使う
- ただし、「w をそのまま使う」のではなく、いったん u(w) に通してから期待値を取る
つまり頭の中では、「まず各パターンの“満足度”を計算する」→ 「その満足度の期待値が高い方を選ぶ」という流れになっています。
なるほど。『お金をそのまま平均』じゃなくて『いったん“うれしさカーブ”を通してから平均』に変えただけってことね。
そういうこっちゃ。ホモエコのルール（期待値で比べる）は残したまま、頭打ちだけ人間寄りにしたのが修正派や。
3-2. ここまでで説明できること
この「凹カーブ」を入れるだけで、かなりそれっぽくなる現象もあります。代表例がこれ。
確実な3,000円 vs 80%で4,000円→ 多くの人が「確実な3,000円」を選ぶ
純血派の世界（直線効用）だと、どちらも期待値は同じ or ほぼ同じなら「より期待値が高い方」で決まりなんですが、頭打ちカーブを通すと、
- 大きな金額を「ギャンブルで増やす」より
- 「確実にもらえる」方の“効用の安心感”が効いてくる
ので「ちょっとだけ多くもらえるかもしれない不確実な選択」より「少し少なくても確実な選択」を好みやすくなる、つまり利得側でのリスク回避は、ここまでで一応説明がつきます。
3-3. それでもまだ説明できない「人間の謎ムーブ」
ただ、ここで終わらないのが人間のめんどくさいところ。まだ説明しきれないものがゴロゴロ残ります。
同じ ±1万円でも「損」の方が圧倒的に痛い（損失回避）
1万円得するとうれしいでも1万円失うと「うれしさの1.5〜2倍くらい痛い」みたいな “損の方が重い”感じ は、「頭打ちの凹カーブ」だけでは出てきません。
損失を見た瞬間に出てくる「ヤケクソモード（リスク愛好）」
利得の場面ではわりと堅実（リスク回避）なのに損失の場面では途端に 「このまま確実に損するくらいなら、一発逆転狙ったろか」と急にギャンブルに走るこの「得ではビビるのに、損では一気に博打打ちたくなる」挙動も、修正派の考えだけでは再現できません。
宝くじ・保険・レア事故：低確率イベントの“盛り方”
宝くじのごく低確率でも「なんかワンチャンありそう」と感じる、ほぼ確実に得する話「99%大丈夫」と言われても、「ゼロじゃないなら…」と日和る。これは 「確率そのものの感じ方」がおかしい話なので「お金側のカーブ」だけいじっても追いつきません。
たしかに、「お金のうれしさに頭打ちがある」ってだけじゃ、日常で見る“変な人間ムーブ”全部は説明できへんな…。
せや。修正派はあくまで「ホモエコの枠組みはそのままに、その中でギリ人間ぽくしてみた」くらいの立ち位置や。ここからこれらの矛盾を説明するのがプロスペクト理論や。
3-4. 第3章のまとめ（この時点の限界）
ここまでで押さえておきたいのはこの3点です。
- 修正派ホモエコは、「お金のうれしさには頭打ちがある」という人間味をu(w)=w^α という凹カーブで表現した
- その結果、利得側でのリスク回避（確実な得を選びがち）までは説明できる
- しかし依然として、損失回避やリスク愛好、低確率イベントの異常な盛り上がりといった「人間の謎ムーブ」まだ残っている
次の第4章から、いよいよプロスペクト理論の核心に入っていきます。ここで一気に、先程列挙した“謎ムーブ”がS字カーブの中に収まり始めます。
第4章 プロスペクト理論の価値関数 v(Δw)｜損失回避とS字カーブ
ここからが本題。ホモエコ業界の内輪ルールから一歩外に出て、「実際の人間」を数式でとらえに行ったのが、プロスペクト理論（Prospect Theory）です。
4-1. まず「見るもの」を変えた：w ではなく Δw
プロスペクト理論の一撃目はここです。
「最終的にいくら持ってるか」じゃなくて、“ある基準からどれだけ増えた／減ったか（Δw）”を考える
数式で書くとこうなります。
Δw = w − w₀
- w₀：参照点（現状、期待していた水準、直前の価格…など）
- Δw > 0：その参照点から見て「得した」
- Δw < 0：その参照点から見て「損した」
ここでのポイントは、同じ「手取り30万円」でも
- 20万円から昇給して30万円になった人にとっては「＋10万円の世界」
- 40万円から減給して30万円になった人にとっては「−10万円の世界」
- w=30万は同じでも、Δwはまったく違う
という「参照点依存」です。
たしかに。給料30万って数字そのものより、「前より増えたか減ったか」の方が気持ちに直撃するわ…。
せやろ？ホモエコは w（最終的な富）だけ見てたけど、人間は Δw（基準からの増減）で世界を見とる、という発想転換がここや。
4-2. 価値関数 v(Δw)：得・損・ヤケクソを1本のS字に
次に、「Δw をどう感じるか」のカーブを見に行きます。人間に山ほど選択問題を解いてもらうと、ざっくりこんなパターンが浮かび上がってきました。
- 利得側ではリスク回避→ 確実に3,000円を選びがち（第3章で出てきたやつ）
- 損失側ではリスク愛好→ 確実に1万円失うより、「ワンチャン失わない賭け」に出たがる
- 損得のうち、損の方がずっと重く感じる→ 1万円得する嬉しさより、1万円失うショックの方がデカい
これらを1本の曲線に押し込んだのが、あの有名なS字カーブです。
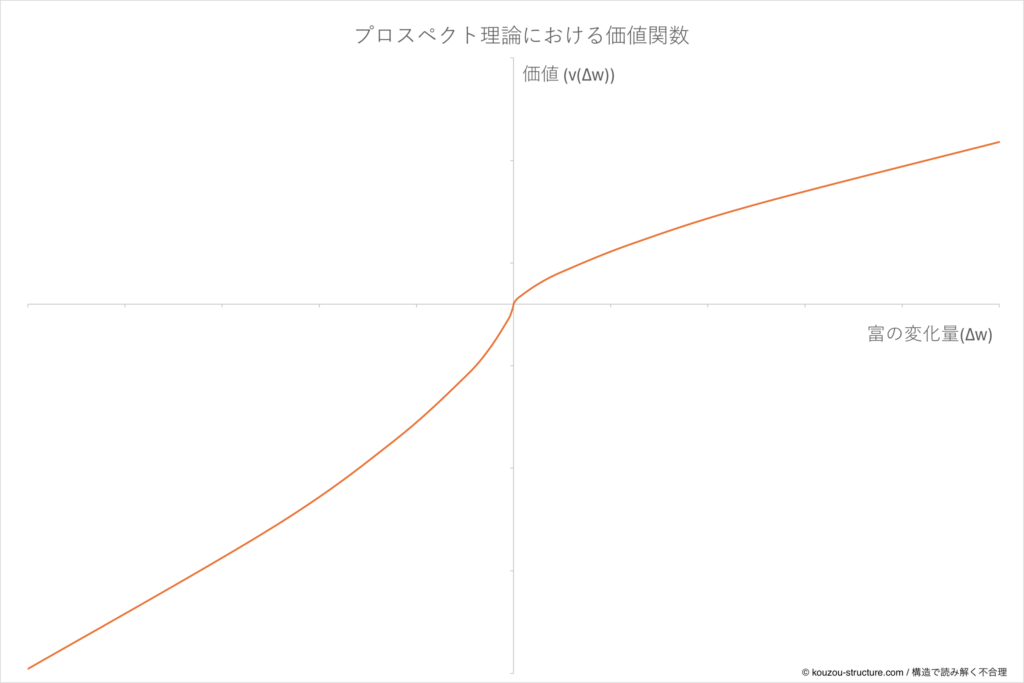
イメージするとこんな感じ：
- 横軸：Δw（基準からの増減）
- 縦軸：v(Δw)（感じている価値・満足度）
- 右側（利得）は「上に凹んだカーブ」
- 左側（損失）は「下に凸のカーブ」で、しかも急に落ちる
数式で書くと、原論文はこんな形を使っています。
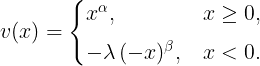
4-2-1. α・β・λ：S字を決める3つのツマミ
さて、ここからがプロスペクト理論の面白いところです、数式を見るとα、β、λが定数となっていることが読み取れます。それぞれのこれら3つのパラメータがあの有名なグラフの形を規定するわけです。
■ α（アルファ：得側の「頭打ち」）
- プラスのΔwに対して、右側のカーブをどれだけ下に押さえつけるか
- 最初のプラスは効くけどだんだん「増やしても増やしても、効きが鈍くなる」
- 行動レベルでは → 利得側のリスク回避 を作っているパラメータ
■ β（ベータ：損側の「ヤケクソカーブ」）
- マイナスのΔwに対して、左側のカーブをどれだけ上に持ち上げるか
- 小さい損はめちゃくちゃ痛いでも、大損ゾーンに入ると「これ以上増えても、もはや誤差」みたいな状態に
- 行動レベルでは → 損失領域でのリスク愛好（ヤケクソモード） を生み出す
■ λ（ラムダ：損の「重み付け」）
- 原点（Δw=0）のところで、損失側だけ急にストンと落とす役割
- 同じ ±1万円でも、「損の方をどれだけ重く感じるか」を決めるツマミ
- 行動レベルでは → 損失回避（loss aversion） そのもの
つまり、α・β・λで「得」「損」「ヤケクソ」の3つの感情パターンを、1本のS字カーブの中に押し込んだわけね。
そういうこっちゃ。で、このツマミの位置は机上で適当に決めたんやなくて、人間に山ほど選択肢を見せて、その“ズレ方”から推算した値なんや。
4-2-2. カーネマン＆トヴェルスキーが見出した代表値
実証研究では、Tversky & Kahneman (1992) の代表的な推定値として、だいたい次のような数字がよく引用されます。
- α ≈ 0.88（得側の頭打ち）
- β ≈ 0.88（損側の曲がり方）
- λ ≈ 2.25（損の重み）
ざっくり読むと、
- 得と損、それぞれの「感度の鈍り方」（αとβ）はわりと似ている
- ただし 損は同じ額の得の2倍以上重く感じている（λ ≈ 2.25）
というイメージになります。です、このあとの６章でも触れますが、この値はカーネマンとトヴェルスキーが人間による実験からはじき出した値。実験デザインや、個々人により値は変動すると思った方が良いですね。
ここから皆さんの感覚に訴える感じで行きます。３つの数字がグラフの形を規定することはわかったと思うので、実際にこれら定数を変動させたグラフを提示します。実はEXCELで記載できるそれほど難しくない仕事です。
4-2-3. α・β・λをいじると、人間の性格がどう変わるか
ここまでで、α・βはカーブの「曲がり具合」、λは損の「重さ」、をざっくり見てきました。ここからは実際にパラメータを動かしたグラフを見ながら、「数値が変わると、人間の性格がどう変わるか」を眺めてみます。
① α・βを動かしてみる（頭打ちとヤケクソの強さ）
まずは α と β を動かして みます。原著論文では 0.88 が出てきますが、グラフの“寝ていく感じ”が直感的にわかりづらいので、ここではわざと
α＝β＝0.60, 0.65, 0.70
の3パターンで描いています（λは 2.25 で固定）。
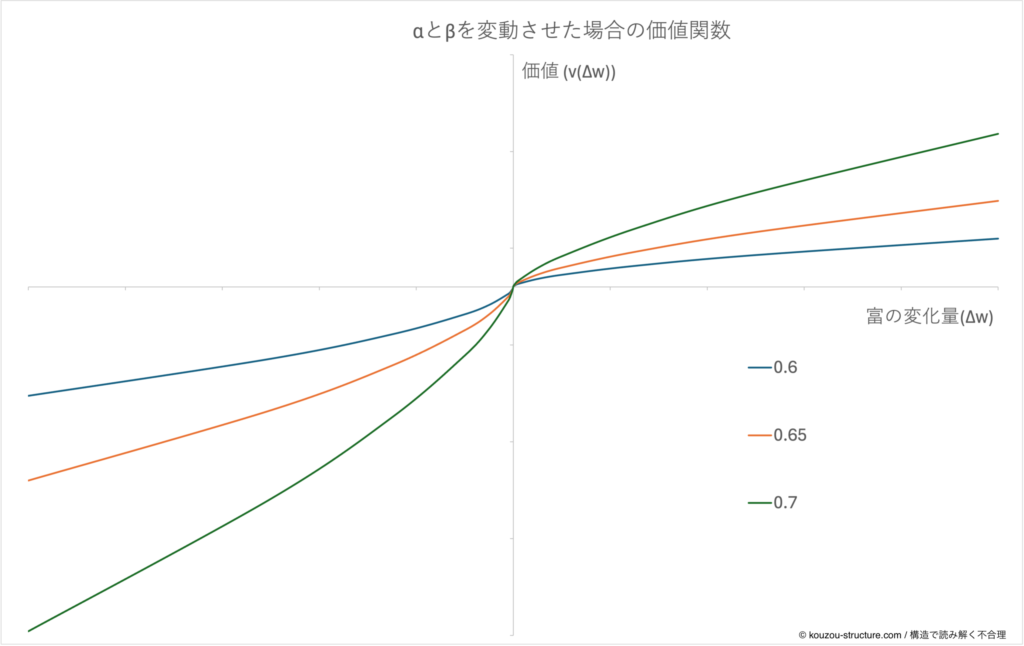
- 同じ Δw（富の変化量）でも、値が小さいほどグラフが縦方向にギュッと圧縮されているのがわかると思います。
- これは、「ちょっと増えた／減っただけで、すぐ効きが鈍る」＝頭打ち（得）とヤケクソ（損）が出やすい ということです。
ざっくり言うと：
- α・β が小さい人→ 少しの得で満足しやすいけど、少しの損でもすぐ感度が鈍る「短気＆飽きっぽいカーブ」
- α・β が1に近い人→ ほぼ直線寄り。得も損もかなり“ホモエコ寄り”の性格
② λを動かしてみる（損失回避の強さ）
次に、損失回避 λ を動かして みます。
ここではα＝β＝0.65 で固定し、λ＝1.25, 2.25, 3.25の3パターンを書きます。
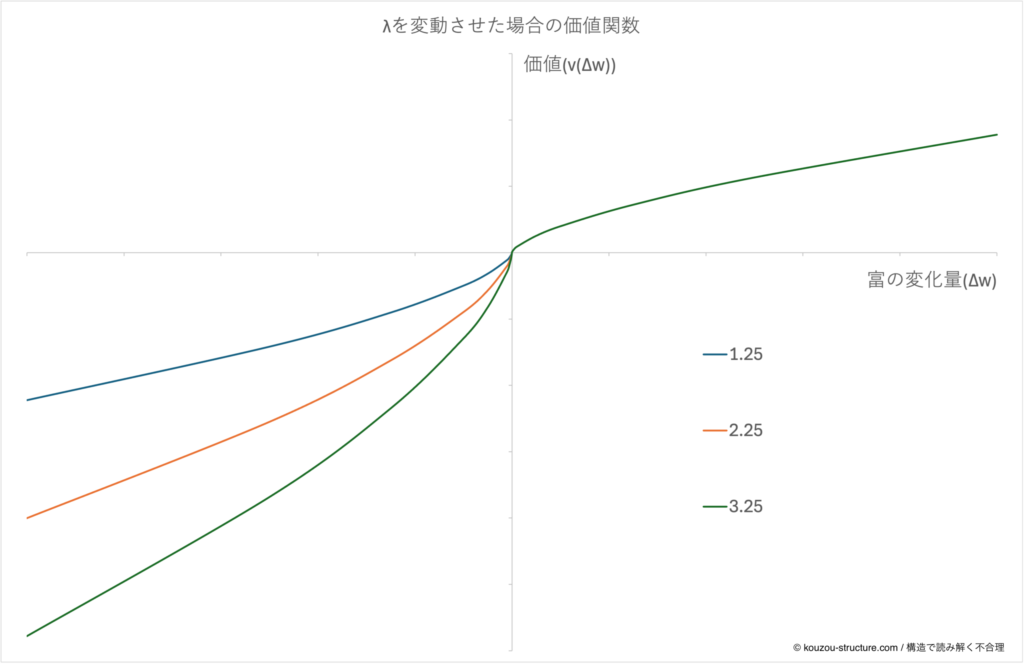
- 利得側（右側）のカーブは どの λ でもピッタリ重なる はずです。
- 一方で損失側（左側）のカーブだけ、λ が大きいほど急角度でストンと落ちる 形になります。
読み方としては：
- λ が大きい人→ 同じ1万円の損でも「メンタルダメージがデカい」＝超ビビり型損失回避強め
- λ が小さい人→ 損への耐性が高く、「まあこのくらいなら…」と受け流しやすいタイプ
なるほど。α・β が「カーブの曲がり方（頭打ち／ヤケクソの出やすさ）」、λ が「損の重さ（ビビり具合）」って感じで、人の性格パラメータみたいに見えてくるな。
そういうこと。ここまでくるとα・β・λ の組み合わせ＝“その人の得・損のクセ”をざっくり数値で表してる、ってイメージが持てると思うで。
このような価値関数は実はEXCELでかけます。ぜひご自身でもチャレンジしてみて下さい。そして数式で人間特性を説明しようとした試みのすごさを味わってみて下さい。
4-3. ここまでで押さえておきたいポイント
- 「wそのもの」ではなく「Δw(参照点からの増減)」を見る世界に切り替えた→ これでフレーミング効果や「同じ30万円でも人によって意味が違う」が自然に説明できる。
- 価値関数 v(Δw) をS字カーブにした
- 右側(得):頭打ち(利得側リスク回避)
- 左側(損):ヤケクソカーブ＋０点から右の急降下(損失回避＋損失側リスク愛好)
- α・β・λは”机上の思いつき”ではなく、実験データから推算されたツマミ→ 「人間がどれだけビビるか／ヤケクソになるか」を、数値でつまみにした<のがプロスペクト理論の価値関数パート。
次の第5章では、いよいよもう片方の主役である 「確率の歪み π(p) と γ」 に入っていきます。
ここで「宝くじ」「レア事故」「99%でも日和る」が、S字カーブとつながりながら、ちゃんと数式の中に収まっていきます。
第5章 プロスペクト理論の確率重み関数 π(p)｜低確率を盛りすぎる人間
ここまでは価値×確率のうち、価値だけ、つまり どれだけ得した／損したかの感じ方 だけをいじってきました。次は確率の感じ方 の番です。
プロスペクト理論はS字カーブが有名すぎて、確率のカーブはスルーされがちです。でもここも同じくらい大事。一緒噛み砕いていきましょう。
5-1. 人間は p をそのまま信じない
純血派・修正派ホモエコたちは、確率をこう扱っていました。「起こる確率 p を、そのまま価値に掛け算して平均を取ればええやろ」と。
- p = 0.01 は、いつでもどこでも「1%」
- p = 0.99 は、いつでもどこでも「99%」
それ以上でもそれ以下でもない。確率はただの数字 という世界観です。でも、人間にいろんな選択問題を解いてもらうと、どうもそうなっていません。
- 宝くじ→ 1/100万でも「なんかワンチャンある気がする」
- レアな事故・病気→ ほぼ起きないのに「怖すぎるから保険入っとくか…」
- 「ほぼ確実に得する案件」→ 「99%大丈夫」と言われても「でもゼロじゃないなら安全側で…」と日和る
データを積んでいくと、ざっくりこんなクセが見えてきます。
- 小さい確率は盛る（過大評価）
- 大きい確率は削る（過小評価）
この「確率の感じ方のズレ」を一発で表現するために、確率重み関数 π(p) というものが導入されます。
5-2. 確率重み π(p)：p をそのまま使わず、一回ねじる
イメージとしては、確率重みとは人間が「効き目」として感じている方の確率
同じ p でも、心の中ではこう変形されています。数式で書くとこんな感じです（詳しくは追わなくてもOK）
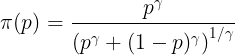
この関数を通すと、
- p が小さいとき：π(p) > p → レアイベントを「起こりそう」と感じる（宝くじ・レア事故など）
- p が大きいとき：π(p) < p → 99%を「なんか不安」と感じる（ほぼ確実な得でも日和る）
ざっくり言うと「p をそのままではなく、ちょっと曲げた版に変換してから使っている」とだけ押さえてもらえれば十分です。
グラフにすると、逆S字（上凸→下に凸） になります。カーネマン＆トヴェルスキー自身も 1992 年の論文で、開区間 (0,1) の中では比較的なだらかで、端点付近（0と1の近く）で急に立ち上がると書いていて、図でも 0%・100%ぴったりの点はわざと切り落として 描かれています。（数学的にいうと、端っこで傾きがバカみたいに大きくなるイメージ）
せやから、プロスペクト理論ではpをそのまま使わへんねん。まず p を一回 π(p) に通してから、価値 v(Δw) と掛け合わせて評価するっていう二段構えにしてるんや。「低確率の事故や当たりの“怖さ／ワンチャン感”」を、きちんと数式にねじ込むためやな。
※本記事では、確率重みについて1979年論文での decision weight の πᵢ と、1992年論文での重み関数 w⁺(·), w⁻(·) をまとめて扱うため、記号を π(p) に統一しています。なお本文中では w を wealth（富） に使っているため、読者の混乱を避ける目的も兼ねて、確率重み関数には w ではなく π を用いています。
5-3. γ（ガンマ）：怖さの強さを決めるツマミ
1992年の累積プロスペクト理論（CPT）では、実は
- 利得側の確率重み関数：w⁺(p)
- 損失側の確率重み関数：w⁻(p)
と、得と損で別々の重みカーブ を使っています。それぞれの「曲がり具合」を決めるパラメータとして、論文では 0.61 と 0.69 といった数字が出てきます。細かい記号は一旦まとめて、ここでは γ（ガンマ） というツマミだと思ってください。
ざっくり言うと：
- γ = 1 のとき
- π(p) = p
- → 逆S字が消えて、ホモエコ世界（確率はただの数字）に戻る
- γ < 1 になるほど
- 逆S字が強くなる
- → 低確率をより盛り、高確率をより削る
イメージとしては、γ が小さいほど「怖がり＆ワンチャン好き」 になります。
- 宝くじ→ γ が小さい人ほど「いや、なんか当たりそう」感が強い
- レア事故・レア病気→ γ が小さい人ほど「自分に起こりそう」感が増す
- ほぼ確実な得→ γ が小さい人ほど「でもゼロじゃないやろ…」と日和りやすい
5-3-1. γ をいじると確率の感じ方はこう変わる
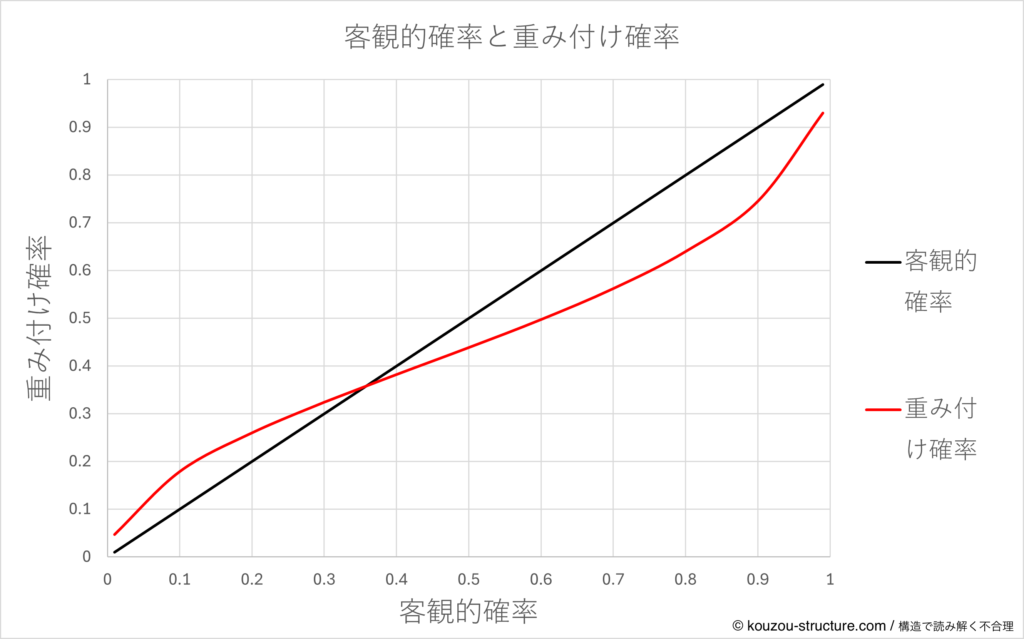
ここで、γを変動させたグラフを提示します。
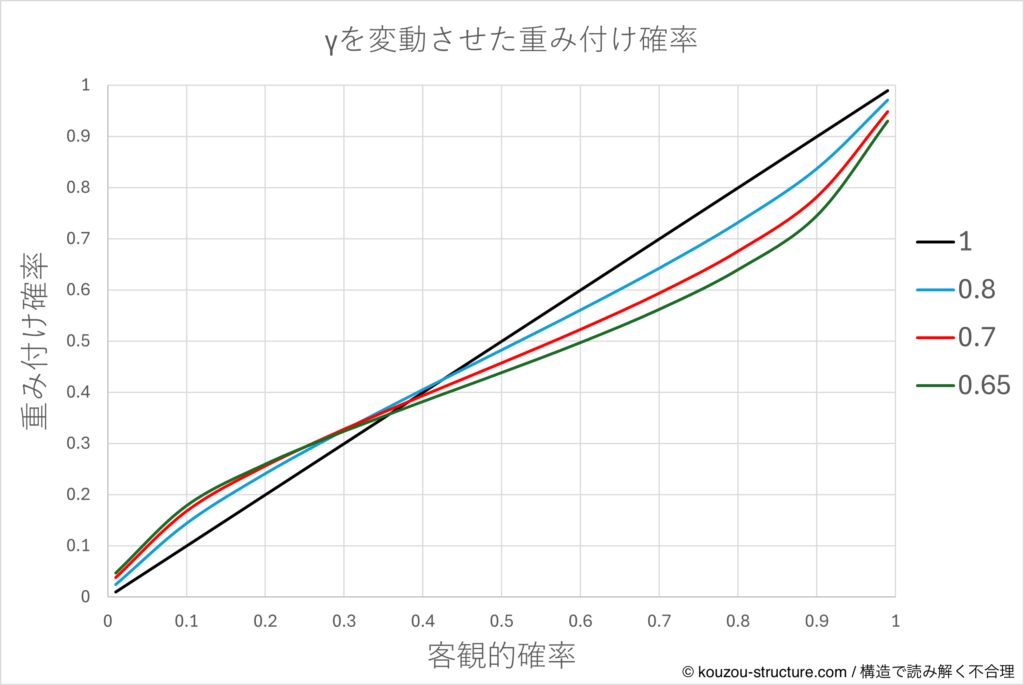
- 横軸：客観的な確率 p
- 縦軸：重み付け後の確率 π(p)
- 黒線：γ = 1（ホモエコ。p をそのまま信じる人）
- 水色・赤・緑：γ = 0.8, 0.7, 0.6（だんだん「怖がり＆ワンチャン好き」）
見ての通り、
- 0〜0.2あたりの低確率ゾーンでは γ が小さい（緑）ほど π(p) が p より上 に来ています。 → 宝くじの「1/100万でも、なんか当たりそう」感はここ。
- 0.8〜1.0あたりの高確率ゾーンでは γ が小さいほど π(p) が p より下 に沈みます。 → 「99％大丈夫」と言われても「でもゼロじゃないし…」と日和るのがここ。
- 真ん中付近（0.3〜0.6）では どの線もあまり変わらず、ほぼ45度線に近いままです。 → ふつうの確率はそこそこ素直に受け取っていて、おかしくなるのは「すごく低い／すごく高い」ところだけ、というイメージですね。
γ を下げる＝曲線を強くする、というのは「レアケースを盛り、高確率をビビって削るクセをどれだけ持っているか」の強さを調整するツマミだと考えるとわかりやすいと思います。
ここは原典の扱いをだいぶ簡素化しているので、最後のコラムで追加します。
簡素化部分を補足した記事を書きました→なぜ宝くじは“当たりそう”で、99％でも日和るのか？確率重み関数で読み解くプロスペクト理論
5-4. ここまでのプロスペクト理論の評価ルール（ざっくり版）
ここまでくると、プロスペクト理論の評価の流れはこう整理できます。
- 価値関数
- 「いくら持ってるか w」ではなく、「基準からどれだけ増減したか Δw」を見る
- その感じ方は S字カーブ v(Δw)（α・β・λ で形が決まる）
- 確率
- 「起こる確率 p」をそのまま信じず、π(p) という“効き目としての確率” に変換する
- その曲がり具合は γ で決まる（逆S字の強さ）
- 最終的な評価
- 各パターンについて「価値 v(Δw) × 効き目としての確率 π(p)」 を計算してどれを選ぶか決めている
つまり、
- 価値で α・β・λ が「得・損・ヤケクソ」
- 確率で γ が「怖さとワンチャンへの弱さ」
を決めていて、その掛け合わせの合計で「どの選択肢がどれだけ魅力的か」を計算してる、ってことね。
そういうこと。ここまで来ると、宝くじも保険も「99%でもモヤる日和り」も、かなりの部分が V = v(Δw) と π(p) の組み合わせ で説明できるようになるわけや。
- 人間は確率 p をそのまま信じない
→ 小さい確率を盛り、大きい確率を削るクセがある。
- そのクセをまとめて表現するのが確率重み関数 π(p)
→ 「数字としての p」ではなく、「効き目としての確率」。
- γ（ガンマ）は逆S字の強さを決めるツマミ
→ γ が小さいほど「怖がり＆ワンチャンに弱い」性格になる。
- プロスペクト理論の評価は、
価値 v(Δw)（S字）と確率の歪み π(p)（逆S字）を掛け合わせて足し合わせる
→ これで、宝くじ・保険・レア事故・「99%でも日和る」などの謎ムーブが、かなりきれいに数式の中に収まる。
次の第6章では、「そもそもα・β・γ・λなんて、どうやって思いついたん？」という話に入ります。
実はこれらは、最初から用意された「きれいな数式」ではなく、先に実験データがあって、そのズレ方を説明するために後から付けられた“調整ノブ”だ、というところを見ていきます。
第6章 プロスペクト理論のパラメータ αβγλ｜人間のクセを蒸留した4つのノブ
ここ、多くの解説書がサラッと流すところだけど、一番おいしい“裏話ゾーン”です。「α・β・γ・λなんて、どうやって思いついたん？」「カーネマンが机の上で“いい感じの数式”をでっち上げたん？」
…と勘違いされがちなんだけど、実態は真逆です。最初にあったのは不合理な選択のデータ。その変な選択データの山を説明するために、あとから調整として α・β・γ・λ を付けた
ノーベル賞のプレスリリースも、プロスペクト理論は公理から演繹したんじゃなくて、実験観察から帰納的に作られたモデルだとはっきり書いてます。
6-1. 出発点は「期待効用からの系統的なズレ」
カーネマン＆トヴェルスキーがまずやったのは、ひたすら選択実験。
- アレのパラドックス（Allais paradox）
- フレーミング（「生存率90%」vs「死亡率10%」）
- 損失回避（＋x と −x の感じ方の非対称）
- 反射効果（利得：リスク回避／損失：リスク愛好）
- 低確率イベント（宝くじ、レア事故、保険…）
みんなに紙の上で「どっち選ぶ？」を延々やってもらい、回答を集めてグラフ化していった。そこで見えたのは、期待値的にはこう選ぶはずが、同じ方向に、何度も・何パターンでもズレ続けるという、きれいに“系統だったズレでした。
- 「確実」は好きだけど、確実な損は余計つらく感じる
- 小さい確率の大当たりや大損を、やたら重く見る
- 得と損で、リスクの取り方がひっくり返る
6-2. α・β：データから逆算した「曲がり具合ノブ」
まずは横軸（得・損）側の形から。
実験データを「参照点＝0」を真ん中にしてプロットすると：
- 利得側（右） → 右肩上がりだが、だんだん寝ていく（凹）
- 損失側（左） → 左下がりだが、だんだんゆるくなる（凸）
- しかも、原点近くが一番キツいカーブになっている
これをシンプルに書ける関数として採用されたのが、
- 0 < α < 1 → 利得側で 凹（だんだん頭打ち）
- 0 < β < 1 → 損失側で 凸（最初のショックがデカい）
ここ、誤解されがちなんやけどな。「まず α と β っていうカッコいいパラメータを決めて、そこに人間を当てはめた」んやなくて逆や。先に“このくらいの曲がり方してるよね”ってデータがあって、あとから「じゃあここを α・β って呼ぼか」と名付けた調整ノブなんよ。
Tversky & Kahneman (1992) の代表的な推定では、α ≈ β ≈ 0.88 あたり。「得も損も、感覚としては“1よりちょい小さめのべき乗”っぽい曲がり方」をしている、というイメージです。
6-3. λ：ゼロでの「折れ目」をどうしても入れざるを得なかった
次の決定打が、損失回避のデータです。実験をすると、ほぼいつもこうなります：
- ＋1万円：みんな、そこそこ嬉しい
- −1万円：同じ額なのに、嫌がり方が段違い
ノーベルプレスは、「中くらいの損の重みは、同じ額の得のおよそ2倍」くらいだとまとめています。グラフで見ると、
- 原点（参照点）で、損側だけ急激に立ち上がる
- つまり、ゼロのところに“折れ目”が必要
そこで入ったのが λ（ラムダ）
- λ > 1 にすると
- 損側のカーブが縦にギュッと伸びる
- 「同じ1万円でも、損側のほうがずっと重い」が再現できる
Tversky & Kahneman (1992) の推定値は λ ≈ 2.25。人は損を、同じ額の得のおよそ 2 倍以上キツく感じるという“人間の感覚の比率”を、そのまま数式に貼り付けた形です。
なるほど。α・β が「カーブの丸まり具合」、λ が「損側だけの増幅率」ってイメージね。
そう。S字の“形そのもの”は α・β が決めて、真ん中の折れ目の左右の“高さの非対称”を λ で合わせてる感じやな。
6-4. γ：低確率と高確率の「ズレ方」に合わせた確率ノブ
残るのが 確率の変な扱い方です。実験をまとめると、ザックリこんな傾向が出ます。
- 小さい確率の大当たり・大損 → やたら魅力的／怖い（宝くじ・レア事故）
- ほぼ確実に得する話 → 変にビビって日和る（確実性効果）
これを期待効用理論みたいに「p をそのまま掛ける」だけでは再現できない。そこで導入されたのが、確率重み関数 π(p) と、その曲がり具合を決める γ です。
- γ = 1 → π(p) = p（ホモエコ世界に戻る）
- γ < 1 → 逆S字が強化
- 小さい p：π(p) > p で盛る
- 大きい p：π(p) < p で削る
Tversky & Kahneman (1992) では、
- 利得側の曲率 ≈ 0.61
- 損失側の曲率 ≈ 0.69
といった推定が報告されています。繰り返しですね。
ここも α・β・λ と同じでな。「低確率をどれだけ盛ってるか」「高確率をどれだけ削ってるか」
っていう“ズレ方”を、あとから γ ってつまみ一個でまとめたって理解が一番しっくりくるで。
6-5. まとめ：αβγλは「人間のクセを蒸留した4つのノブ」
ここまで整理すると、プロスペクト理論のパラメータはだいたいこう見えます。
- α・β
- 利得・損失それぞれの 「潰れ具合」
- データから見えた S字の凹凸を、べき乗で近似したもの
- λ
- 参照点での 「損のほうがキツい」折れ目の非対称
- 損失回避の強さ（おおざっぱに「約2倍」）
- γ
- 確率の逆S字の 「盛り／削り」の強さ
- 宝くじ・保険・レア事故・確実性効果をまとめてチューニングするノブ
要するに、価値のグラフ（α・β・λ） と確率の歪み（γ）をいじることで、「期待値からのズレパターン」がほぼ再現できるようにした、ってことか。
せやねん。ノーベル委員会の言い方を借りれば、これは“公理から導いた理想像”じゃなくて、実験で見つかった“現実のクセ”を真面目に数式に写し取ったモデルってことや。αβγλは、そのクセを4つのつまみにギュッと圧縮した“人間のツマミセット”やと思っといてくれたらええ。
- 出発点は数式ではなく「期待効用からの系統的なズレ」
アレのパラドックス、フレーミング、損失回避、低確率イベント…→ どれも同じ方向に外れ続けるデータがまずあった。
- α・β はグラフの曲率から“逆算された”ノブ
→ 利得は凹、損失は凸を、べき関数で近似（α ≈ β ≈ 0.88）。
- λ はゼロでの「損だけキツい」折れ目を入れる係数
→ 損は同額の得の ≒2倍重く感じる（λ ≈ 2.25）。
- γ は確率の逆S字の強さを決めるノブ
→ 低確率を盛り、高確率を削るクセ（γ ≈ 0.6〜0.7）。
- プロスペクト理論 = 実験データから帰納的に作られた“人間のクセ関数”
→ αβγλは、机上の空論ではなく、観察された謎ムーブを説明した調整パラメータ。
第7章 実験経済学とプロスペクト理論｜カーネマンとバーノン・スミスの接点
ここまでで、個人レベルの意思決定 をプロスペクト理論で追いかけてきました。じゃあ同じ年にノーベル経済学賞を取った バーノン・スミス は、どこで響き合っているのか。プロスペクト理論を解説する記事で、ここに触れている記事はほとんどないので、噛み砕いていきましょう。
7-1. スミスがやったこと：市場そのものの「風洞実験」
スミスの仕事をざっくり一言にすると、「市場を実験室に持ち込んで、ルールを変えながらどう動くかを計測した人」です。やっていたことをもう少し分解すると、こんな感じ。
- オークションの形式を変える
- 一番高い人が落札する「普通のオークション」
- 2番目に高い人の価格で落札する「セカンド・プライス・オークション」…など
- 参加者が持っている情報を変える
- みんなが同じ情報を持つケース
- 一部の参加者だけが有利な情報を持つケース
- インセンティブ設計を変える
- どれだけ利益を出せたかで報酬を変える
- 指定のルールに従ったときだけ報酬が出る…など
こうやって条件をいじりながら、
- 価格がどこに収束するのか
- どれくらい効率的に取引が行われるのか
- どんな条件でバブル・クラッシュが起こるのか
を実験で確かめていきました。
要するに「理論上こうなるはずの市場」を、実験室の中で実際に動かしてみた人ってことか。
そういうこっちゃ。飛行機の理論だけ語っててもしゃあないから、風洞に入れて翼の形試す、みたいなノリやな。
7-2. カーネマンとの共通点：「理論から」じゃなく「データから」曲げる
ここからが、カーネマンとの一番おいしい接点です。まず、伝統的な経済学の流れをざっくり整理すると：
- まずホモ・エコノミクス前提で「こう振る舞うはず」というきれいなモデルを立てる
- データはそのあとで、「理論が合ってるか検証するため」に使う
という順番でした。それに対して——
■ カーネマン＆トヴェルスキー側
- まず実験で人の選択データを集める
- 「期待値的にはこう選ぶはず」から同じ方向にズレ続けるパターンを見つける
- そのズレを説明するためにプロスペクト理論を構築した
■ スミス側
- まず実験室で市場を動かしてみる
- ルール・情報・インセンティブを変えたときに、価格や取引量がどれだけ理論値とズレるか、どんな条件だと効率が落ちるかを実測する
- その結果を踏まえて、「競争市場はどの条件までうまく機能するのか」「どんな制度設計ならうまくいくのか」といった市場理論・制度設計の考え方を調整する
どちらもやっていることは、同じパターンにまとめられます。
実験（ラボ）で人や市場の振る舞いを観察 →そこから逆算してモデル（数式）を曲げ直す
この 「実験 → モデル」ループ を、カーネマンは個人の意思決定で、スミスは市場全体の振る舞いで、それぞれ確立したわけです。
7-3. ノーベル賞を「セット受賞」として読む
つまり、「カーネマンは“人”をラボに連れてきて、S字グラフを引き出した人」「スミスは“市場”をラボに連れてきて、制度の効き方を引き出した人」っていう並びになるわけね。
そう。で、この二人を同じ年にノーベル賞にしたのがポイントやとワイは思っとる。
- ホモ・エコノミクスの頭の中だけで完結させる時代は終わりにしろ
- 人間と市場をラボに連れてきて、ちゃんと測れ
- そのデータに合わせて、理論や数式のほうを曲げ直せ
──ノーベル委員会のプレスリリースを読むと、だいたいこういうメッセージが透けて見えます。
- スミスは「市場そのものの実験」を確立した人
→ オークション形式・情報・インセンティブを変えつつ、市場の動きを実験室で観察。
- カーネマン＆トヴェルスキーも、まず実験からスタート
→ 人の選択のズレを観察し、その結果に合わせて αβγλ を含むモデルを設計。
- 両者に共通するのは「理論→検証」ではなく「実験→モデル」の流儀。
- 二人の同時受賞は、「経済学をホモエコの頭の中から、実験データに基づく科学へ引きずり出す」という方向転換の象徴と読める。
次の最終章では、ここまでの話をもう一度まとめ直して、
- 純血派ホモエコ
- 修正派ホモエコ
- プロスペクト理論（＋実験経済学）
が、一枚の構造図の上でどう配置されるのかを整理していきます。
第8章 まとめ｜ホモ・エコノミクスとプロスペクト理論の違いを一枚に整理
ここまで出てきた話を、最後に一枚の構造として並べ直しておきます。「どの理論が」「どこまで人間っぽさを拾えていて」「どこから先がプロスペクト理論の領域か」をハッキリさせる回です。
8-1. 三つの世界を一枚に並べる
まずは、第2章〜第5章までに出てきた「三つの世界」の整理から。
| 世界 / 派閥 | 見ているもの | 価値の形 | 確率の扱い | 説明できること |
|---|---|---|---|---|
| 純血派ホモエコ | 最終的な富 w | 直線：u(w)=w | p をそのまま | 「期待値が高い方を選ぶ」だけ |
| 修正派ホモエコ | 最終的な富 w | 凹曲線：u(w)=w^α | p をそのまま | 利得側のリスク回避 |
| プロスペクト理論 | 参照点からの変化 Δw | S字：得側凹・損側凸・原点で折れ目 | p→π(p) に変換 | 損失回避・サンクコスト・フレーミング・宝くじ／保険の挙動 など |
プロスペクト理論の一番のポイントは、ここです。
- 「最終的な富 w」という発想をいったん横に置いて、
- 「参照点からの変化 Δw」＋「確率の歪み π(p)」
という二つの非線形プロセスに分解したこと。
同じ「30万円」でも、昇給30万と減給30万は全然違うし、「1％」でも宝くじと重病リスクじゃ意味が違う。その“体感の歪み”を、ちゃんとモデル側で折り込んだのがプロスペクト理論ってことね。
せや。ホモエコは「w と p はそのまま信じるもんや」という前提で粘ったけど、プロスペクト理論は「いや、人間の頭の中では、その時点ですでに曲がっとるやろ」と開き直ったわけやな。
8-2. 人間の非合理をいじる 4 つのツマミ：α・β・γ・λ
ここまで出てきたパラメータを、「どこをいじるノブなのか」という視点で一枚にしておきます。
| パラメータ | 何をいじる？ | 行動的意味（ざっくり） |
|---|---|---|
| λ（ラムダ） | 損失側の傾き（ゼロ付近の落ち方） | 損の重さ。「損は得の2倍以上痛い」を作る |
| α（アルファ） | 利得側の曲率（右側の凹み具合） | 得の頭打ち。ちょい得は効くが、だんだんテンション鈍る（利得側リスク回避） |
| β（ベータ） | 損失側の曲率（左側の凸具合） | ヤケクソカーブ。大損ゾーンで「ここまで来たら一発逆転やろ」になる（損失側リスク愛好） |
| γ（ガンマ）※コラム参照 | 確率の歪みの強さ（逆S字の曲がり具合） | 怖さとワンチャンへの弱さ。低確率を盛り、高確率をビビって削る |
ここで大事なのは、こいつらが
- 「きれいな数式を作りたいから」先に置かれたパラメータではなく、
- 実験で観測された“ズレ方”をグラフに描いてから、あとづけで名前を付けた補正ノブ
だという点です。
α・β・γ・λは、「人間がおかしい」ってラベルやないで。「ホモエコの直線からどの方向・どれくらいズレてるか」を、数値でつまみにしたもんやと思ってくれたらええ。
なるほど。「人間は非合理」ってディスるんじゃなくて、「ズレのパターンがむしろ一貫してるから、パラメータで記述できる」と見たのが、プロスペクト理論の発想ってことね。
8-3. だから、この理論とこの二人でノーベル賞
最後に、カーネマン＆トヴェルスキー（＋プロスペクト理論）と、バーノン・スミス（実験経済学）をまとめて眺めます。
■ カーネマン側で起きたこと
- 個人の意思決定レベルで、「ホモエコの直線」→「人間のS字＋逆S字」へとモデルを曲げ直した
- その過程で α・β・γ・λ を導入し、1979年にプロスペクト理論の枠組み（参照点・S字カーブ）を提示し、1992年に累積版（CPT）として、確率重みとパラメータ推定を精緻化
- 「人はホモエコではない」という直感を、実験データ＋数式でちゃんと土台にした
■ スミス側で起きたこと
- 市場レベルで、「理論上の綺麗な市場」を実験室に引きずり下ろした
- オークション形式・情報構造・インセンティブをいじりながら、どの条件なら競争市場がうまく機能するのか、どんな制度やルールだとバブル・非効率が出るのかをラボで実測した
- 「市場はこう振る舞うはず」という教科書の話を、条件付きで現実に繋ぎ直した
この二人をセットで見ると、だいたいこう読めます。
経済学は、ホモエコの頭の中だけで完結させる時代から、人間と市場の「実際の振る舞い」を測りに行き、そのデータに合わせてモデルを曲げ直す実証科学へ
プロスペクト理論がノーベル賞を取った意味は、決して「新しい関数の形がかっこよかったから」
ではなく、ホモエコの直線を、人間のS字グラフ＋確率の逆S字に変えたこと、そしてその変え方の流儀が、スミスの実験経済学と同じく 「実験 → モデル」ループ に乗っていたこと、という、経済学そのものの方向転換にあります。
- ホモエコ＝「w と p をそのまま信じる直線世界」
- 修正派ホモエコ＝「w の側だけちょっと凹ませた世界」
- プロスペクト理論＝「Δw と π(p) に分解して、人間のS字と逆S字をフル装備した世界」
そして、その背後には
- α・β・γ・λで“ズレのパターン”を数値化したカーネマン
- 市場そのものをラボに入れて「理論を現実に繋ぎ直した」スミス
という二人の仕事がセットで走っている。
この構造さえ掴んだら、行動経済学の他のトピック（メンタルアカウンティング、ナッジ、ヒューリスティクス論争…）を読むときも、「これは、ホモエコのどこをどう曲げ直した話なのか？」という視点で、かなり気持ちよく整理できるはずです。
コラム：本当は γ だけじゃなくて δ もいる話（確率重みまわり）
この記事では説明をシンプルにするために、
- 確率重み関数：π(p)
- 曲率パラメータ：γ（ガンマ）
とだけ書いていますが、原典（Tversky & Kahneman, 1992）ではもう一段ちゃんと分かれています。ざっくり言うと：
- 利得側の重み関数：w⁺(p)
- 損失側の重み関数：w⁻(p)
と、得と損で別々のカーブを使い、それぞれに別のパラメータ
- 利得側の曲率：γ
- 損失側の曲率：δ
を付けています。推定値は以下の通り。
- γ ≈ 0.61（利得側）
- δ ≈ 0.69（損失側）
本記事では、
- 「小さい確率を盛り、大きい確率を削る」という逆S字のイメージ
- 「その曲がり具合を決めるツマミ」としての “γ 的なもの”
だけ伝えたかったので、w⁺/w⁻ や δ の違いを一度まとめて “γ” に潰して書いています。厳密にやると、利得と損失で関数を使い分けますが、本記事では直感優先でかなり簡略化しています。
コラム：Σ の中身をかなり雑に書いてます（累積部分の省略）
本文ではプロスペクト理論の評価ルールを
V(a) = Σ π(pᵢ) · v(Δwᵢ)
みたいな形で書いていますが、これは かなりラフに潰した書き方 です。原論文の 累積プロスペクト理論（CPT） では、本当はもっとややこしくて、
- 利得と損失を分ける
- 結果を「良い順／悪い順」に並べる（ランクづけ）
- そのランクに応じて 累積確率 をとる
- その累積確率を関数に通して 「決定ウェイト（decision weight）」 を作る
- その決定ウェイトを係数として Σ を取る
…という流れになっています。
ぶっちゃけると、筆者もこの decision weight あたりから先は「雰囲気はわかるけど、数式としては追い切れてない側の人間」 です。「ああ、順位づけした上で、確率をまとめてグニャッと重み付けしてるのね」くらいの理解で止めています。この記事では、
- 「価値が S 字カーブになる」
- 「確率が逆 S 字カーブになる」
- それを「掛け合わせて足し合わせる」
という 直感の骨格だけを押さえる のを優先して、「累積」や「決定ウェイト」の正確な定義は、あえて書いていません。ちゃんとした数式レベルまで込みで CPT を理解したい方は、Tversky & Kahneman (1992) の原典を直接読みに行ってください。
ここは「ブログで直感をつかんでもらうための簡略版」として、専門家の方には「だいぶ削っているな」と理解したうえで読んでもらえると助かります。
【引用・転載について】
学術目的やレポート等での参照・引用は大歓迎です。その際は、出典として当記事のタイトルとURLを明記してください。なお、本文の全文転載や大部分の無断転載はご遠慮ください。
参考文献
- Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47(2), 263–291.
- Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5(4), 297–323.
- The Royal Swedish Academy of Sciences. (2002). The Prize in Economic Sciences 2002 – Press release (Daniel Kahneman and Vernon L. Smith). NobelPrize.org.
コメント