導入｜「99%大丈夫」なのに、なんかモヤる
今回の記事は「人間の不合理はこう曲がる｜プロスペクト理論を数式と原典からガチ解説」
のスピンオフ記事です。プロスペクト理論の確率重み関数に絞って解説していきます。
実は上記の記事はダニエル・カーネマンとエイモス・トヴェルスキーが見出した「確率の歪み」を意図的に簡略化して書いておりました。今回はこの歪みをもっと深堀りし、日常に落とし込めるように解説します。そして前回と同様、数式は出しますが、それを見なくとも理解できるように進めます。
人間の「ワンチャン狙い・日和り」を噛み砕いていきましょう。
専門家の方へ（ご挨拶とお願い）
本記事では、プロスペクト理論の「直感の骨格」を一般向けに伝えることを優先し意図的な単純化・ラフな書き方 をしています。学部〜大学院レベルで勉強されている方から見ると、「そこはもう少しちゃんと書けるやろ」というところが多々あると思いますが、「非専門家がプロスペクト理論の根幹を見に行く踏み台」という位置づけで割り切って構成しました。もし 明らかにミスっている箇所 や、「ここだけはさすがに誤解を生む」というポイントがありましたら、お手数ですがご指摘いただけると大変ありがたいです。可能な限り原典に沿う形で順次修正していきます。
この記事でわかること
- 人は、確率 p をそのまま信じているわけではない（小さい確率は盛り、大きい確率は削る）
- プロスペクト理論の「確率重み関数」π(p) と、逆S字カーブのざっくりした意味
- 宝くじのワンチャン感は「低確率ゾーン」、99％で日和るのは「高確率ゾーン」の話
- 利得側（γ≈0.61）と損失側（δ≈0.69）で歪みの強さが違う＝得するときほどバグる
- 本編で「γ的なもの」とまとめていた部分の、もう一歩踏み込んだ話
第1章 人はpをそのまま信じない：ワンチャンと日和り
1-1 宝くじ・ゲーム・ほぼ通る稟議
確率の数字そのものは理解しているはずなのに、私たちの行動はその通りになりません。
- 上司から「この稟議は95％通るから大丈夫」と言われても、決裁ハンコがつくまではソワソワする
- ゲームで「命中率95％」と表示されていても、「なんか不安」といって確実な技を選ぶ
- 一方で、宝くじの1/100万は「ほぼ0」だとわかっているのに、売り場の前に立つと「ワンチャンあるかも…」と財布に手が伸びる
冷静に考えたら「1/100万なんてほぼ0やろ」なんやけど、宝くじ売り場の前に立つと、なんか当たりそうな気がしてくるんよな。
それがまさに「確率そのもの」やなくて、「効き目としての確率」π(p) を見てる状態や。
この「効き目としての確率」π(p)こそが、プロスペクト理論でいう確率重み関数の主役です。人間は、教科書に書かれた客観的な確率pをそのまま感じるのではなく、頭の中でいったん”盛ったり削ったり”してから判断に使っています。
1-2 「数字としての p」と「効き目としての π(p)」
まず、用語だけサクッと整理しておきます。
- p：確率（probability）：サイコロで1が出る確率1/6、ガチャの排出率1％、降水確率10％。こういった「客観的に与えられた数字としての確率」です。
- π(p)：確率重み（weighted probability）：人間が実際の判断で使っている、「効き目として感じている確率」。さっきの宝くじやゲームの例で言うと、
- 宝くじのpは「ほぼ0」なのに、π(p)は「なんかありそう」に盛られてしまう
- ゲームの命中率95％のpはかなり高いのに、π(p)は「8割ちょいくらい？」に削られてしまう
プロスペクト理論では、このp → π(p)への変換を確率重み関数という形で表します。グラフで描くと、「逆S字」のカーブになります（ここではイメージだけでOK）：
- 左下（小さい確率）のところで、客観的確率より上にふくらむ → レアイベントを盛る
- 右上（大きい確率）のところで、客観的確率より下にへこむ → ほぼ確実なイベントを削る
本編でも出てきたやつやね。pをそのまま使わず、一回ねじってから使う、っていう。
せや。この記事では、その「ねじり方」をもうちょい細かく見ていくで。特に、
- 低確率ゾーンの”ワンチャン盛り”
- 高確率ゾーンの”99％日和り”
- しかも「利得のときの方が、損失のときよりバグりやすい」
って話まで踏み込むつもりや。
私たちは「数字としての確率 p」ではなく、「効き目としての確率」を感じている
- 稟議「95％通る」は頭ではわかっていても、決裁まではなぜかソワソワする
- ゲームの命中率95％はわかっているけど、安全策を取る
- 宝くじ1/100万は「ほぼ0」と知りつつも、「ワンチャンあるかも」と感じてしまう
このズレを表現するために、
- 客観的な確率：p
- 頭の中で感じている”効き目としての確率”：π(p)（確率重み）
と区別して考える。
このあと第2章では、
- 具体的にどんな形の関数でこの「逆S字」を表現しているのか
- その曲がり具合を決めるγ（ガンマ）とδ（デルタ）がどう効いてくるのか
を、数式は最小限にしながら噛み砕いていきます。
第2章 確率重み関数 π(p)：逆S字の正体
第1章では、「客観的な確率」p と「効き目として感じている確率」π(p) を区別し、人間は p をそのまま使っていないという話をしました。第2章では、その「ねじり方」の中身を、できるだけ直感的に見ていきます。
2-1 ざっくり関数だけ出しておく（見た目だけでOK）
原典（Tversky & Kahneman, 1992）では、利得・損失で関数を分けつつ、わりとゴツい式が出てきます。ここでは、「こういうタイプの関数を使ってます」という顔見せだけしておきます。
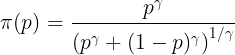
π(p) = p^γ / 〔 p^γ + (1 − p)^γ 〕^(1/γ)
- 0 < p < 1
- 0 < γ ≤ 1
見た瞬間に「おい数式出すな」となった人は、安心してください。この式を追えなくても、この記事の本筋は問題なく理解できます。ここで大事なのは、以下の2点だけです。
- π(p) は p をそのまま使わず、いったん「曲げる関数」に通したもの
- γ（ガンマ）が、その「曲がり具合」を決めるツマミになっている
正直、この式をいきなり見せられても「へぇ〜」以上の感想が出てこんのやけど…。
それでええねん。「この式を使ったからエラい」んやなくて、
- 小さい確率は盛る
- 大きい確率は削る
- それを一発で表せるような曲線にした
ってことだけ伝われば、この章の目的は達成や。
2-2 直線と逆S字を頭の中で見る
グラフのイメージを、共有しておきます。こちらは以前のプロスペクト理論の解説記事で使用した重み付け確率です。
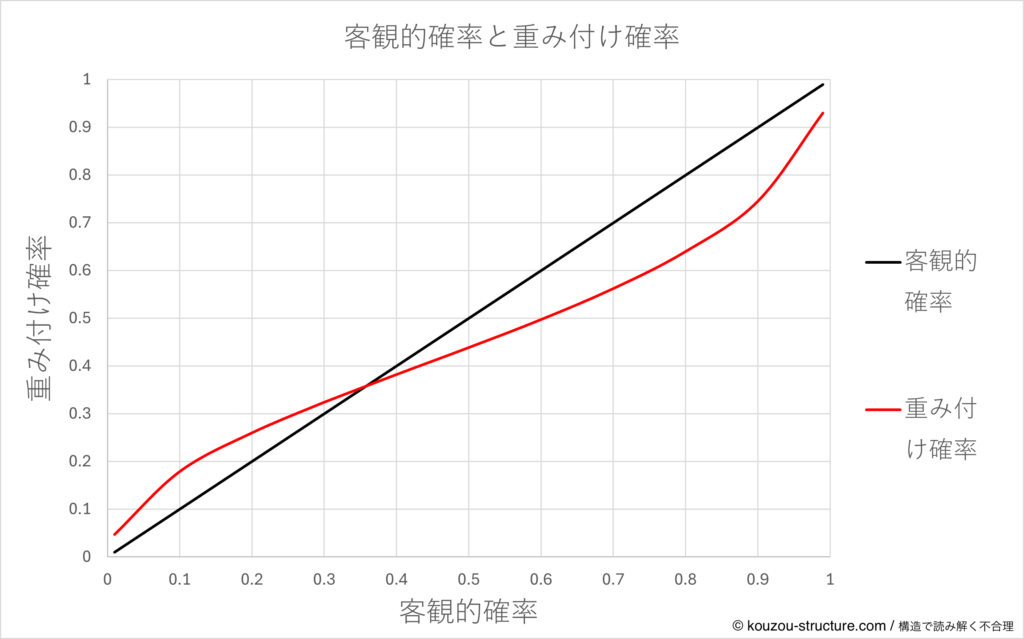
- まず、何もしない場合（ホモ・エコノミクス世界）
- 横軸：客観的な確率 p（0〜1）
- 縦軸：評価に使う確率
- 「p をそのまま信じる人」は、原点から右上に伸びる直線になります。この線は π(p)=p の世界。つまり「数字で出された確率を、そのまま信じるホモエコ」です。
- 人間の π(p) を重ねるとどうなるか
- 小さい確率のところ（0〜0.3くらい）で、カーブが直線より上にふくらみます → レアイベントを盛って感じているゾーン
- 大きい確率のところ（0.7〜0.9くらい）で、カーブが直線より下に沈みます → ほぼ確実なイベントを削って感じているゾーン
あー、なんとなくイメージできた。「宝くじゾーン」と「99％日和りゾーン」が、直線からグニャッとずれてるわけね。
せや。で、その「ずれ具合」を決めてるのが γ ってわけやな。
※原典では、0％と100％ぴったりのところは、わざと外して描かれています。数学的にはそのあたりの扱いがややこしくなるので、この記事でも 0＜p＜1 の範囲だけをイメージの対象にします。
2-3 γ（ガンマ）＝逆S字の「曲がり具合」ツマミ
ここでようやく γ の出番です。ざっくり言うと、γ は、「どれくらい強く p を盛ったり削ったりするか」を決めるノブだと思ってください。
■ γ = 1 のとき
さっきの式に γ=1 を入れると、π(p) = pとなります。つまり、小さい確率も大きい確率も真ん中の確率もほぼそのままの数字として受け取っている人、というイメージです。いわゆるホモ・エコノミクスに該当します。
■ γ < 1 のとき
γ が 1 より小さくなるほど、逆S字の「カーブ感」が強くなります。具体的には：
- 低確率ゾーン（p が小さいところ）で π(p) が p より大きくなる → レアな当たり／レアな事故を 盛って感じる
- 高確率ゾーン（p が 1 に近いところ）で π(p) が p より小さくなる → 「99％大丈夫」と言われても 日和って削る
γ が小さい人ほど「怖がり＆ワンチャン好き」ってことか。
そういうことや。宝くじ・ガチャの「ワンチャンあるやろ」感が強く出たり、「ほぼ通る稟議」や「命中率95％」でも、なぜかモヤモヤするっていう “盛る”と“日和る”の両方が強めに出る性格 になるのが、γ が小さい人やな。
2-4 本編とのつながり：ここではあえて「γ ひとつ」に潰している話
ここでプロスペクト理論本編の簡素化の部分です。実はカーネマンとトヴェルスキーが見出した確率荷重の「ツマミ」は実は２種類あったのです。
- 利得側（得する話）の場合：γ
- 損失側（損する話）の場合：δ
これを意味するところは、「人は得する場合と損する場合で確率の感じ方が異なる」ということです。でも、２章までは
- 「人は p をそのまま信じない」
- 「逆S字の曲線で盛ったり削ったりしている」
- 「その曲がり具合を決めるツマミが γ 的なパラメータ」
という 直感の土台 を固めるのが、この章の役割。利得と損失で γ/δ がどう違うのか、「得のときの方が、損のときより確率判断がバグりやすいのか？」という話は、第3章でちゃんと分けて扱います。
- 人は、確率 p をそのまま使わず、確率重み関数 π(p) に通してから判断している
- π(p) のグラフは「逆S字」：
- 小さい確率ゾーン → 直線より上（レアイベントを盛る）
- 大きい確率ゾーン → 直線より下（ほぼ確実な出来事を削る）
- 真ん中ゾーン → 直線に近く、わりと素直
- γ（ガンマ）はこの逆S字の「曲がり具合」を決めるツマミ：
- γ = 1 → π(p) ≒ p（ホモエコ的、ほぼフラット）
- γ < 1 → 低確率を盛り、高確率を削るクセが強くなる
- γ が小さいほど、「怖がり＆ワンチャン好き」な確率感覚になる
次の３章で利得と損失で γ/δ がどう違うのか、を具体的な数字も軽く眺めつつ、「得するときほど確率判断がバグる」 という直感を、図とストーリーで確認していきます。
第3章 得するときほどバグる？γとδの違い
第2章では、小さい確率は「盛る」、大きい確率は「削る」——その逆S字カーブの曲がり具合を決めるツマミがγだというところまで押さえました。ここから一歩踏み込んでいきます。
利得（得する場面）と損失（損する場面）で、このツマミの値が実は違っているという話です。ざっくり言うと、同じ50％でも「得の賭け」と「損の賭け」で、効き目として感じている確率が違うということを、γとδを使って表現しています。
3-1 原典の数値：γ≈0.61、δ≈0.69
Tversky & Kahneman (1992) では、利得と損失で別々に確率重み関数を推定しています。細かい推定方法の話は飛ばして、結果として出てきた数値だけつまみ食いするとこうなります：
- 利得側の曲率：γ ≈ 0.61
- 損失側の曲率：δ ≈ 0.69
ここで思い出したいのが第2章のポイント：
- γ（あるいはδ）が1に近いほど → まっすぐ（π(p)≒p）
- γ（あるいはδ）が小さいほど → 逆S字がきつくなる
つまり、この数字から読み取れるのはシンプルです。数値の小さい利得側のほうが、確率の歪みが大きいということです。これを図示したのが以下のグラフです。
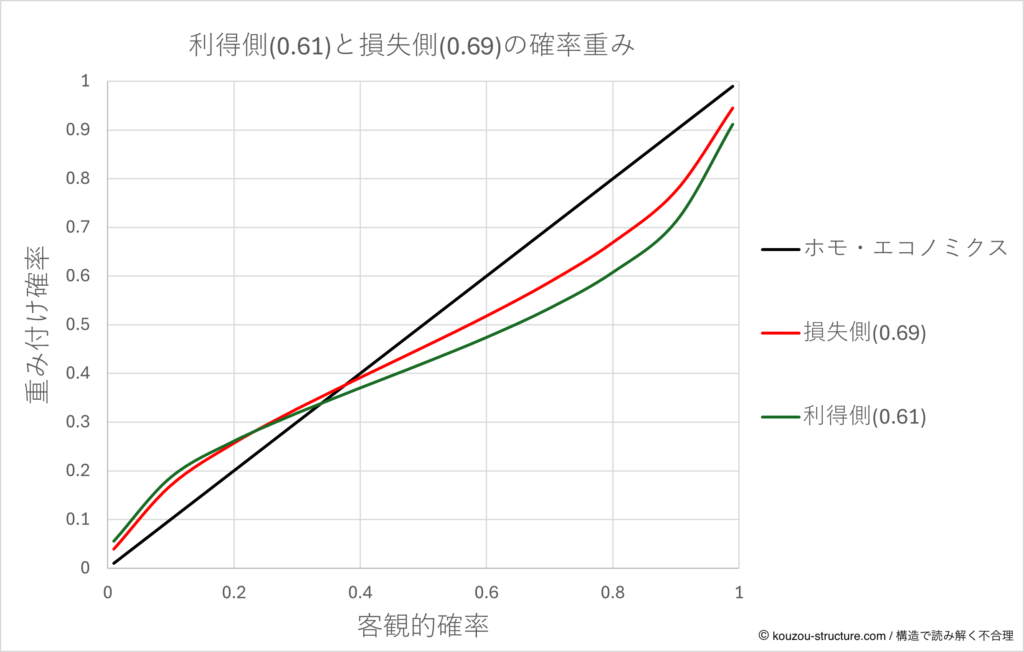
見ての通り、客観的確率0.8〜0.9くらいのところでそれぞれの違いが一番出ていますね。ホモ・エコノミクスとの差は最大で利得で約19%、損失で約13%ほど。利得と損失の差は最大約6%ほどです。
この0.61と0.69という数値自体もカーネマンとトヴェルスキーが人間を元にしたデータからはじき出した数値なので、人や実験デザインよって差はあります。それでも一つ言えるのは、
人間は損するときのほうが確率を正確に見積もる（それでも客観的確率よりだいぶズレている）
ということでしょう。
ちょっと待って。得と損で、確率の”バグり方”も違うん？
せや。γ < δ ってことは、利得側のほうが「より歪んでる」ってことになる。
逆に損失側は、ちょっとだけ冷静ってこと？
「冷静」というより、「確率のバグり方はまだマシ」くらいのニュアンスやな。ただ、こっちはこっちで価値関数の損失回避 λ≈2.25 も効いてくるから、また別の意味でバグってるけどな。
確率の歪み γ/δ と、価値の歪み λ、両方からバグってるってことか…。
せや。で、その掛け算が「人間の選択」として出てくるわけや。プロスペクト理論はその両方を一緒にモデル化したところがミソやねん。
- プロスペクト理論では、利得と損失で別々の確率重み関数を使う：
- 利得側の曲率：γ ≈ 0.61
- 損失側の曲率：δ ≈ 0.69
- γ / δ が1より小さいほど、逆S字が強くなり、
- 小さい確率を盛る（レアイベントを過大評価）
- 大きい確率を削る（ほぼ確実でも日和る）
- γ < δ ということは、
- 利得側の方が、確率の「盛る／削る」が強く出る
- 言い換えると、「儲かりそう」「得しそう」な話ほど、確率判断がバグる
- その差は最大6％くらい
- 損失側も逆S字はあるが、「確率のバグり方」は利得より控えめ。それでもバグる
- 別途、損失回避パラメータ λ が別ルートでガツンと効いてくる
第4章 日常の4マスで見る「確率の歪み」
ここまで、
- 人は「確率 p」をそのまま使わず
- 「効き目としての確率」π(p) にねじってから判断している
- そのねじれ方が、逆S字カーブと γ・δ で表せる
という話をしてきました。この章では、日常の4つの場面に落とし込んでいきます。
- 利得（得）× 低確率
- 利得（得）× 高確率
- 損失（損）× 低確率
- 損失（損）× 高確率
この4マスです。
この4分割は、『ファスト＆スロー』でカーネマンが提示したパターンと同じです。同書では訴訟など日本では馴染みの薄い例で説明されていたので、本記事ではもっと日常にフィットした例を使います。
4-1 利得 × 低確率：宝くじ・ガチャの「ワンチャン感」
まずは一番わかりやすいマスから。利得 × 低確率。
- 宝くじ 1/100万
- ソシャゲのガチャ排出率 0.5％
- 懸賞の「ご当選は1名様」
頭では「ほぼ0」とわかっているのに、売り場やガチャ画面を前にすると「いや、ワンチャンあるかも……」と、ゼロじゃないという事実だけで盛り上がってしまう。
確率だけ見たら「一生引いても当たらんレベル」なのに、なんか「今日はいけそう」って思うんよな……。
ここで起きてるのが、
- 客観的な p（0.005 とか 0.000001）より
- π(p) が上にふくらむ ＝「低確率の利得を盛る」ってやつやな。
逆S字カーブでいうと、このゾーンは左下のふくらんでる部分。
- p はほぼゼロ寄り
- でも π(p) は「数％くらいありそう」と感じる
だからこそ、「一攫千金ビジネス」や「激レア排出」が商売として成立する。
【コラム：宝くじは「無視」か「爆盛り」か？──カーネマンが認めた”数式の限界”】
ここで鋭い読者なら、ある矛盾に気づくかもしれません。「おい、低確率を盛るなら、なんで俺たちは『隕石が落ちてくる確率』にはビビらずに暮らせてるんや？」
確かに数式（確率重み関数）上、確率が0に近づくほど急激に跳ね上がります。もし脳が常にこの数式通りに動いていたら、私たちはあらゆるレアなリスク（隕石、未知のウイルス、通り魔）に怯えて、家から一歩も出られなくなるはずです。
実はカーネマンたちも、1979年の論文でこの問題に触れており、「編集段階（Editing Phase）」という概念で説明しています。
編集段階？ 動画編集みたいなもんか？
似たようなもんや。脳は複雑な計算をする前に、「細かすぎる情報は四捨五入してスッキリさせる」という下処理（編集）をするんや。
つまり、天文学的な低確率に対して、人間の脳は「2つのモード」を行ったり来たりします。
- 無視モード（四捨五入でゼロ）：「0.000001％？ めんどくさいからゼロってことで！」→ 普段の隕石やレアな病気はこっち。完全に無視。
- 爆盛りモード（スイッチON）：CMやニュースで意識が向いた瞬間、ゼロ扱いが解除され、数式のカーブが発動する。→ 「もしかして、当たるかも」
なるほど。普段は「無視（ゼロ）」やけど、宝くじ売り場で３億円ののぼりが目に入った瞬間に「爆盛り」のスイッチが入るわけか。
せや。極端な低確率は「0か、過大評価か」のどっちかしかない。この不安定さこそが、人間のリアリティなんや。
4-2 利得 × 高確率：95％でも日和る「安全第一」
次は利得 × 高確率。
- 上司：「この稟議は95％通るから大丈夫」
- クライアント：「ほぼ確実に契約いけると思います」
- ゲームの「命中率95％」スキル
数字としてはかなり心強いはずなのに、実際にはこんな気持ちが出てきます。
95％って言われても、「じゃあ20回に1回は落ちるんやろ？」って思うとなんか落ち着かへんのよな。
このとき頭の中では、p = 0.95 やのに体感では π(p) ≒ 0.85 とか 0.9 くらいに削れて感じてるイメージやな。
逆S字カーブでいうと、右上でへこんでいる部分。
- 本当は95％の高確率利得
- でも π(p) はそれより少し低めに感じる
だから、「確実な得」をより好み（確実性効果）、「ほぼ確実」には妙な不安が残ります。
その結果、こんな行動につながります。
- リターンは小さくなっても、「確実にボーナスが出る方」を選ぶ
- ゲームで「命中率95％」の一撃より、「命中率100％だけど威力控えめ」のスキルを選びがち
4-3 損失 × 低確率：レア事故・レア病に「必要以上にビビる」
3つ目は損失 × 低確率。
- 「極めてまれですが、重大な副作用が出るケースがあります」
- ニュースで見るレアな事故・事件
実際の確率はとても小さい。でも損失がデカいせいで、頭の中ではこうなりがちです。
飛行機事故のニュース見たあとって、確率がどうこうより「落ちたら終わりやん」って気持ちになるよな。
ここでも p 自体はかなり小さいのに、π(p) は盛られて感じる。宝くじと同じ「左下ゾーン」やねん。ただしこっちは「得」やなくて損失側の左下。
ポイントは、利得×低確率（宝くじ）も損失×低確率（レア事故）も、どちらも「低確率を盛る」点では同じということ。違うのは感情の中身。前者は「ワンチャン欲しくて盛る」、後者は「最悪を避けたくて盛る」です。
4-4 損失 × 高確率：倒産間近の株を「ワンチャン」で握りしめる
最後が今回、ちゃんと扱いたかったマス。損失 × 高確率、ここでは倒産間近の株の話でいきます。
- 業績ボロボロ
- ニュースもネガティブだらけ
- チャートも右肩下がり
冷静な第三者が見れば、「かなりの確率で、この銘柄はこのまま沈むやろな……」という状況。それでも、実際にその株を持っている当人は、
- 「ここまで下がったなら、もうそろそろ反発するやろ」
- 「新製品が当たれば、ワンチャン復活もあるし」
- 「今売ったら損が確定するから、とりあえず様子見しよ」
と、なかなか手放せません。
頭では「このまま持ってたらほぼ負けやろな」と思ってるのに、「いや、ゼロじゃないし」って言い訳しながら握りしめるあれやな……。
このケース、実はかなりいろんなバイアスのコンボになっとる。
- 「かなりの確率で損失」という 高確率損失をちょっとマイルドに感じる（δ 側の「削り」）
- 一方で、「もしかしたらV字回復するかも」という低確率の利得シナリオを 盛って 感じる（γ 側の「ワンチャン盛り」）
- さらに「ここまで下がったのに今さら売れん」というプロスペクト理論の外枠やけどサンクコスト効果 まで乗ってくるっていう、なかなかの三重苦や。
ここで起きていることを、確率重みの視点でざっくり分解すると：
- 本当の世界：
- 「沈む」シナリオ：高確率の損失
- 「奇跡の復活」シナリオ：ごく低確率の利得
- 頭の中の世界：
- 高確率の損失側 → δ でちょっと 削って 感じる
- 低確率の利得側 → γ でかなり 盛って 感じる
そのうえで、さらに 「ここまで耐えたのに今売るのはもったいない」 という損失回避・サンクコストが背中を押す。
つまり、
- 「負け濃厚」の確率は 現実よりちょい低め に見積もってて
- 「奇跡の復活」の確率は 現実よりかなり高め に盛ってて
- そこに「今さら損確定させたくねえ」っていう感情も乗ってる、
って状態ってことか。
そう。
- δ（損失側の確率重み）
- γ（利得側の確率重み）
- λ（損失回避）＋サンクコスト
が全部ごちゃっと絡んで、「現実よりはだいぶマシな世界」を頭の中に作ってしまっているって見方もできるわけやな。
4-5 4マスを逆S字カーブの上に並べてみる
ここまでの4つを、逆S字カーブの上にざっくり並べ直すと：
- 利得 × 低確率：宝くじ・ガチャ → 左下で盛る（γ 側の「ワンチャン」）
- 利得 × 高確率：95％稟議・命中率95％ → 右上で削る（γ 側の「日和り」）
- 損失 × 低確率：レア事故・レア副作用 → 左下で盛る（δ 側の「最悪を避けたい」）
- 損失 × 高確率：倒産間近株を握りしめる → 本来は右上の「ほぼ確実負け」ゾーンだが、δ でちょい削りつつ、γ・サンクコストまで発動してカオス化
同じ逆S字カーブの上でも、「得か損か」と「高いか低いか」で出てくる行動の顔つきが全然ちゃうの、ちょっと気持ちいいな。
せやろ。この4マスを一回イメージで掴んでおくと、ニュースでも、投資でも、職場でも、「今、自分はどのマスでバグっとるんや？」ってメタ的に眺めやすくなるはずやで。
- 利得 × 低確率→ 宝くじ・ガチャ → 低確率の利得を「ワンチャン」で盛る（左下ゾーン）
- 利得 × 高確率→ 95％稟議・命中率95％ → 高確率の利得を「なんか不安」で削る（右上ゾーン）
- 損失 × 低確率→ レア事故・レア副作用 → 低確率の損失を「最悪を避けたい」で盛る（左下ゾーン、損失版）
- 損失 × 高確率→ 倒産間近株をワンチャンで握りしめる → 本来は「ほぼ確実負け」ゾーンだが、
- 高確率損失を少しマイルドに感じる（δ の削り）
- 低確率の復活シナリオを盛る（γ のワンチャン）
- さらに損失回避・サンクコストまで乗ってカオス化
この4マスを頭に置いて第2章・第3章を読み直すと、数式の「線」が日常の「顔」として見えてくるはずです。
第5章 まとめ：確率を“感じる自分”を一歩引いて見る
ここまで見てきたのは、ざっくり言うと次の3つでした。
- 人は p をそのまま信じていない
- 「客観的な確率」＝ p
- 「効き目として感じている確率」＝ π(p)
- 宝くじのワンチャン感も、95％稟議でソワソワするのも、p → π(p) のねじれの産物。
- そのねじれは「逆S字カーブ」と γ・δ で表せる
- 低確率ゾーン：レアイベントを 盛る（宝くじ・レア事故）
- 高確率ゾーン：ほぼ確実な出来事を 削る（95％案件・「ほぼ勝ち」）
- その曲がり具合を決めるツマミが、利得側 γ と損失側 δ。
- 利得の方が、確率のバグり方が強い（γ ≈ 0.61 < δ ≈ 0.69）
- 得の場面：ワンチャンに弱い・確実な得を過大評価しがち
- 損の場面：確率の歪みは「まだマシ」だが、損失回避 λ とサンクコストが暴れる
- 倒産間近株をワンチャンで握りしめるのは、これら全部の合わせ技。
- 私たちは「確率 p」そのものではなく、ねじれた「効き目としての確率 π(p)」で動いている
- 低確率は盛り、高確率は削る＝逆S字カーブ が、宝くじのワンチャン感と 99％日和りを同時に説明してくれる
- 利得側の γ は損失側の δ より小さい ≒ 得するときほど確率判断がバグる(少しの差だが)
- 損失側は確率の歪みはやや弱いが、損失回避 λ やサンクコストとセットで暴走しがち
- 「今の自分は 4 マスのどこにいる？」と一瞬立ち止まるだけでも、感情に持っていかれ過ぎない意思決定に近づける
5-1 どう使うか：ワンチャン・日和り・握りしめをラベリングする
実務でも投資でもゲームでも、
- 「これ、今ワンチャン盛ってへん？」（利得×低確率）
- 「99％って言われてるのに、変にビビってない？」（利得×高確率）
- 「負け濃厚やのに、倒産株みたいに握りしめてない？」（損失×高確率）
みたいに、自分の感情にラベルを貼るだけでもだいぶ違ってきます。
数式を覚える必要はなくて、「あ、今 γ とか δ とか λ が暴れてるターンやな」ぐらいにメタで眺められれば、それだけでプロスペクト理論を実務レベルで使ってると言っていいと思います。
参考文献
- Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47(2), 263–291.
- Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5(4), 297–323.
補足事項
- 確率重み関数の変遷について 本記事で紹介した数式とパラメータは、1992年のTversky & Kahnemanによる「累積プロスペクト理論（CPT）」に基づいています。1979年の初期プロスペクト理論では、確率重み関数は概念的なグラフとして示されたのみで、具体的な数式は定義されていませんでした。本記事ではわかりやすさを優先し、より精緻化された1992年版のモデルを中心に解説しています。また、本来、累積プロスペクト理論では確率重みは「累積された確率」に対して適用されますが、本記事では直感的な理解を優先し、単純な p → π(p) の形で説明しています。
- 【免責事項】 本記事は行動経済学の理論解説を目的としており、特定の金融商品・投資手法・ギャンブルを推奨・勧誘するものではありません。記事内で取り上げている株式投資や宝くじの事例は、人間の心理的傾向（バイアス）を説明するためのモデルケースです。投資や資産運用に関する最終的な決定は、ご自身の判断と責任において行っていただけますようお願いいたします。本記事の情報に基づいて被ったいかなる損害についても、当方は一切の責任を負いかねます。
コメント